Теоретическое введение. Характеристики движения твердого тела, вращающегося вокруг неподвижной оси, могут быть определены из основного уравнения динамики вращательного движения

Характеристики движения твердого тела, вращающегося вокруг неподвижной оси, могут быть определены из основного уравнения динамики вращательного движения

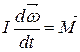, (7.1)

где 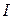– момент инерции тела, 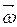– угловая скорость, 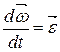– угловое ускорение, 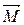– полный момент внешних сил.

Уравнение (7.1) – это второй закон Ньютона для вращательного движения, аналогичный закону движения материальной точки: .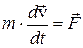

Определить момент инерции абсолютно твёрдого тела можно следующим образом. Все тело мысленно разбивается на совокупность маленьких частичек с массами 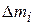( 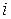– номер частиц), которые можно рассматривать как материальные точки с неизменными расстояниями между ними. При этом 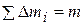- масса всего тела. В результате задача сводится к задаче о вращении системы материальных точек вокруг оси. Из решения ее следует, что момент инерции тела 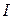определяется таким образом:

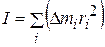. (7.2)

Величина 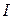равна сумме произведений элементарных масс 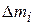на квадрат их расстояний от оси вращения 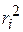. Вектор 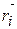лежит в плоскости вращения массы 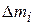и направлен от оси вращения к этой материальной точке. Из определения (7.2) видно, что задание полной массы тела 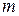еще ничего не говорит о величине его момента инерции 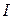, который зависит от того, как расположены различные части 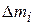тела относительно той или иной оси.

В случае непрерывного распределения массы с плотностью 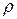сумма в (7.2) заменится на интеграл по всему объему тела. Каждый из элементарных объемов тела 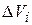массой 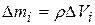при переходе к бесконечно малым заменяем на 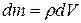, и, соответственно,

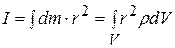. (7.3)

Вычисление момента инерции твердого тела произвольной формы относительно оси представляет собой сложную задачу – необходимо знать, как плотность тела 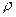меняется от точки к точке 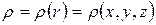. Если эта зависимость известна, тогда нужно вычислить тройной интеграл 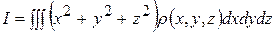. Это несложно делать для однородных ( 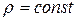) симметричных твердых тел, вращающихся вокруг неподвижной оси, проходящей через центр масс (центр тяжести). Далее будут приведены выражения для моментов инерции шара, цилиндра, пустотелого цилиндра.

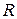Величины моментов инерции чаще определяют из опыта. Рассмотрим, как это можно сделать, решая задачу о скатывании круглого однородного тела радиусом и массой 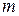без скольжения по наклонной плоскости, расположенной под углом 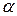к горизонту, с высоты 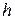(рис. 7.1) с использованием закона сохранения энергии.

Задача о скатывании – пример плоского движения твердого тела, т.е. движения, при котором точки тела описывают траектории, лежащие в параллельных плоскостях. Если ось вращения проведем через центр масс тела (точку О) перпендикулярно плоскостям, в которых лежат траектории точек тела, то ось будет двигаться поступательно, оставаясь параллельной самой себе.

В этом случае кинетическую энергию твердого тела при плоском движении можно представить как энергию вращения вокруг оси, проходящей через центр масс тела, и энергию поступательного движения со скоростью, равной скорости центра масс :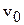

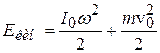, (7.4)

здесь 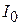– момент инерции тела относительно оси вращения, проходящей через его центр масс, 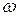– угловая скорость тела, 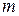– его масса.

Если тело скатывается с высоты 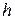, то в соответствии с законом сохранения энергии

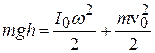. (7.5)

Центр масс тела движется равноускоренно под действием силы трения покоя 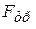и составляющей силы тяжести. Поэтому, если обозначим через 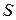длину наклонной плоскости ( 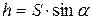) и считаем, что тело движется с нулевой начальной скоростью, то

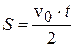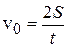; , (7.6)

где 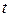– время движения тела по наклонной плоскости. Предполагается, что тело скатывается без скольжения, и поэтому линейная скорость точек соприкосновения тела с наклонной плоскостью равна нулю, так что скорость поступательного движения 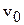связана с угловой скоростью 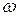обычным соотношением 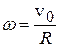. Если теперь подставить выражение для 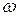и (7.6) в (7.5) и решить это уравнение относительно 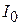, то получим

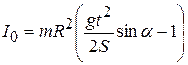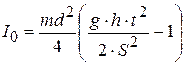, . (7.7)

Это соотношение позволяет, измерив на опыте время скатывания тела 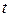, длину наклонной плоскости 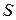, высоту 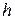, массу тела 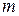и его диаметр 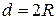, определить момент инерции. В то же время из (7.3) можно теоретически рассчитать моменты инерции шара, цилиндра и пустотелого цилиндра с внутренним и внешним радиусам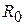и и 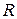соответственно (см.(7.8)) и сравнить их с измеренными значениями.

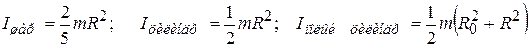. (7.8)

При решении задачи о качении тела предполагали, что силами трения качения можно пренебречь. Поэтому в законе сохранения энергии не учитывали работу этих сил трения. Сила же трения покоя (рис.7.1) как раз и создает вращающий момент относительно оси, проходящей через центр масс тела. В этом несложно убедиться, если получить выражение (7.7), используя не закон сохранения энергии (7.5), а решив систему уравнений для движения центра масс тела и вращательного движения

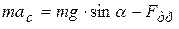, (7.9)

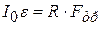. (7.10)

При этом нужно учесть связь ускорения поступательного движения цилиндра при скатывании с угловым ускорением (7.11) и уравнение кинематики равноускоренного движения (7.12):

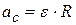, (7.11)

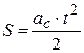. (7.12)

В заключение найдем условие, при котором будет отсутствовать проскальзывание при качении тела. Пусть наше тело – цилиндр. Для него момент инерции 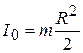. Подставим (7.11) в уравнение (7.10), получим из него и из (7.9) выражение для сил трения

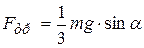. (7.13)

Известно, что в отсутствии скольжения сила трения не должна превышать своего максимального значения (см. также работу 1-06):

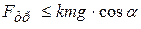, (7.14)

где 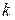-коэффициент трения покоя.

Так что условие непроскальзывания скатывающегося цилиндра:

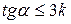. (7.15)

Именно под таким углом 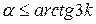следует устанавливать наклонную плоскость при скатывании цилиндра для определения момента инерции.