Моделирование схем электрических сетей с помощью четырехполюсников
Часть электрической цепи, рассматриваемая по отношению к двум парам ее выводов, называется четырехполюсником. Ранее здесь использовалось представление четырехполюсником ЛЭП и трансформаторов, однако существует возможность представления в виде четырехполюсника и соединений этих элементов – схем электрических сетей.
Моделирование четырехполюсником удобно применять тогда, когда предметом исследования являются токи (потоки мощности) и напряжения на его выводах, а не токи и напряжения внутри самого четырехполюсника.
По свойству линейности элементов четырехполюсники разделяют на линейные и нелинейные.
Схема замещения (внутренняя схема соединений) четырехполюсника может быть: Г-образная (рис. 3.16, а), Т-образная (рис. 3.16, б),
П-образная (рис. 3.16, в), четырехплечая (рис. 3.16, г), П-образная мостовая (рис. 3.16, д), Т-образная мостовая (рис. 3.16, е) и др.
Четырехполюсник называется активным, если он внутри содержит источники электрической энергии, и пассивным, если внутри него нет источников энергии.
Различают четырехполюсники симметричные и несимметричные. Симметричным называют четырехполюсник, когда перемена мест его входа и выхода не изменяет токов и напряжений в цепи, с которой он соединен.
Основной смысл теории четырехполюсников заключается в том, что, пользуясь обобщенными параметрами четырехполюсников, можно находить токи и напряжения на входе и выходе четырехполюсника.
Из множества соединений четырехполюсников в электрических сетях применимы только две: каскадное (рис. 3.16, а) и параллельное (рис. 3.16, б).

Рис. 3.16. Схемы замещения четырехполюсника
Электрическая сеть, имеющая в общем случае множество узлов и ветвей, может рассматриваться как совокупность четырехполюсников, соединенных по определенной схеме. Отличительной чертой четырехполюсников, моделирующих элементы электрической сети, является наличие у них всех одного общего полюса – нейтральной плоскости, и по сути они могут считаться трехполюсниками. Сложность схемы соединения электрической сети и нелинейность, вносимая нагрузками и генераторами, не позволяют широко использовать четырехполюсники для моделирования электрических сетей. Возможны два принципиально различающихся подхода к использованию четырехполюсников:
· моделирование отдельных элементов или их каскадно-парал-лельного соединения при отсутствии в них источника энергии или нагрузки, заданных нелинейными математическими моделями;
· приближенное представление части электрической сети при наличии нелинейных моделей генерации или нагрузки в виде эквивалентного четырехполюсника.
Последний подход распространяется на моделирование электрических сетей с помощью многополюсников.

Рис. 3.17. Соединения четырехполюсников:
а – каскадное; б – параллельное
Рассмотрим первый подход. Для получения параметров эквивалентного (результирующего) четырехполюсника, составленного из простых четырехполюсников, параметры которых известны, удобно пользоваться матричной формой записи:
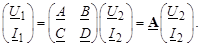 (3.55)
(3.55)
Запись уравнений четырехполюсника (3.54) называется А-формой записи. Другие формы уравнений четырехполюсника могут быть получены из (3.55) выражением в левой части тех или других пар токов и напряжений. Всего возможно шесть форм записи – число сочетаний из четырех по два. Можно выделить еще две формы записи: это Y-форма (3.56) и Z-форма (3.57).
 (3.56)
(3.56)
 (3.57)
(3.57)
При каскадном соединении четырехполюсников (рис. 3.17, а) параметры эквивалентного четырехполюсника получаются перемножением матриц коэффициентов четырехполюсников в A-форме (3.55), а при параллельном соединении (рис. 3.17, б) – сложением матриц коэффициентов четырехполюсников в Y-форме (3.56):
 (3.58)
(3.58)
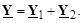 (3.59)
(3.59)
Дата добавления: 2015-03-19; просмотров: 2355;
