Моделирование генераторных узлов электрической сети
Генераторными узлами называют узлы, в которых генерируется активная мощность. Реактивная мощность, как правило, также генерируется в узлах. Генераторные узлы – это шины электрических станций или шины мощной системы, схема которой не входит в модель для расчетной схемы. Моделируются генераторные узлы по-разному:
· так же, как и узел нагрузки, – постоянными значениями активной и реактивной мощности, но с противоположным знаком;
· постоянным значением активной мощности и фиксированным значением модуля напряжения в узле. Реактивная мощность не известна и подлежит расчету;
· генераторный узел – это базисный и балансирующий узел одновременно. Активная и реактивная мощности узла подлежат вычислению;
· генераторный узел – это базисный узел, но с известными значениями активной и реактивной мощности – заданы все четыре независимых параметра режима – P, Q, U, d;
· генераторный узел – это балансирующий узел, но напряжение в нем не известно ни по модулю, ни по фазе. Подлежат определению все четыре независимых параметра режима – P, Q, U, d.
При фиксации активной мощности и модуля напряжения обычно в уравнения установившегося режима входит уравнение для активной мощности узла (3.46) и уравнение вида: 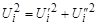 , где Ui задано, а
, где Ui задано, а 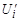 и
и 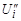 подлежат определению.
подлежат определению.
В тех случаях, когда для одного из узлов требуется задать все четыре независимых параметра режима – P, Q, U, d (базисный узел), то в сети должен появиться узел, в котором не известен ни один из этих четырех параметров – балансирующий узел. Происходит разделение балансирующего и базисного узлов.
Форма уравнений установившегося режима меняется, а именно –перестраивается матрица узловых проводимостей. Так, например, если для графа сети на рис. 3.10 базисным стал узел 2, а балансирующим остался узел 0, то матрица Y принимает вид:
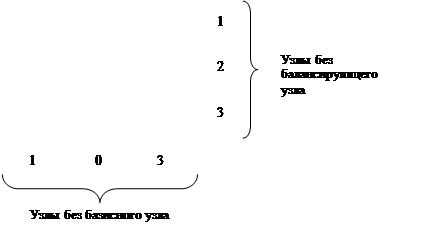
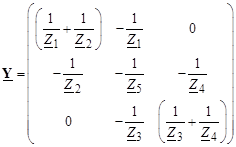
Пример 4. Рассчитаем напряжения в узлах электрической сети (рис. 3.11) при несовпадении базисного и балансирующего узлов.
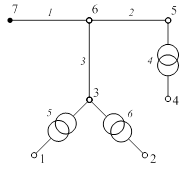
Рис. 3.11. Схема сети примера 4
Ветви 1, 2 и 3 графа – это линии электропередачи 110 кВ, выполненные проводом марки АС-120/19 с погонными параметрами r0 = 0,249 Ом/км;
x0 = 0,427 Ом/км; b0 = 2,6 мкСм/км. Три двухобмоточных трансформатора имеют номинальные напряжение обмоток высшего и низшего напряжения соответственно 115 и 11 кВ.
Параметры линий и трансформаторов приведены в табл. 3.1 и 3.2
Таблица 3.1
Параметры ЛЭП
| Наименование | Начало | Конец | Длина, км | R, Ом | X, Ом | B, мкСм |
| Л-1 | 7,2 | 1,79 | 3,07 | 19,2 | ||
| Л-2 | 3,4 | 0,85 | 1,45 | 9,0 | ||
| Л-3 | 12,3 | 3,06 | 5,25 | 32,7 |
Таблица 3.2
Параметры трансформаторов
| Наименование | Начало | Конец | Тип | R, Ом | X, Ом | DP, кВт | DQ, квар |
| Т-1 | ТМН-6300/110 | 15,99 | 220,42 | ||||
| Т-2 | ТДН-10000.110 | 7,93 | 136,86 | 15,1 | |||
| Т-3 | ТДН-16000/110 | 4,44 | 86,79 | 21,3 |
Мощности нагрузки даны для шин низкого напряжения трансформаторов – узлы 1 (T1), 2 (T2) и 4 (Т3).
PT1 + jQT1 = 5,0 + j2,5 МВ·А; PT2 + jQT2 = 7,0 + j3,5 МВ·А;
PT1 + jQT1 = 12,0 + j6,0 МВ·А.
Приведем два расчета: вначале расчет, когда базисный и балансирующий узлы совпадают – узел 7; затем – балансирующим остается узел 7, а базисным является узел 5. Расчеты выполним в системе Mathcad. Сопротивления в омах, проводимости в сименсах, напряжения в киловольтах, мощности в мегаваттах.
Системная переменная начального номера массивов:
Исходные данные по линиям:
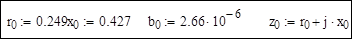
Расчетные данные по линиям:
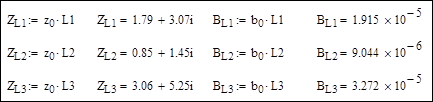
Исходные и расчетные данные по трансформаторам:
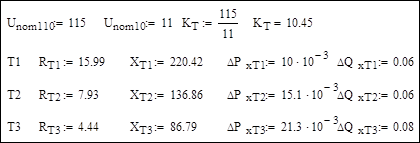
Исходные данные по мощностям нагрузок:
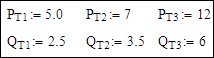
Вектор проводимостей продольных ветвей и вектор проводимостей связи независимых узлов с базисным узлом (в первом расчете – узел 7):
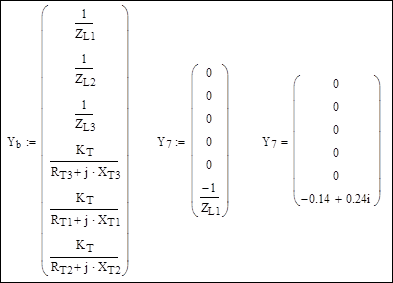
Матрица инциденций M и матрица узловых проводимостей:
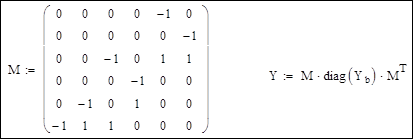
Корректировка диагональных элементов матрицы узловых проводимостей для учета поперечных ветвей П-образных схем замещения линий и трансформаторов:
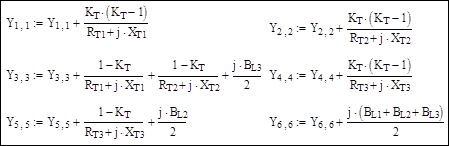
Результирующая матрица узловых проводимостей:
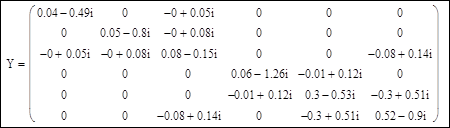
Матрица задающих мощностей в узлах сети:
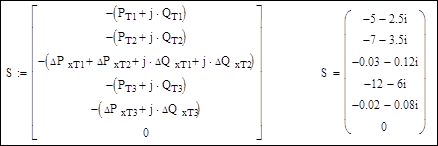
Напряжение в базисном узле и начальные приближения напряжений в узлах:

Решающий блок:
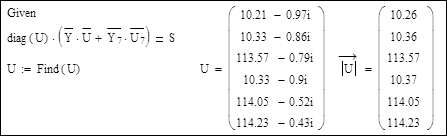
Выполним расчет для случая, когда базисным узлом является узел 5, а балансирующим остается узел 7. Поменяем в матрице Y столбец, соответствующий узлу 5; теперь это столбец проводимостей связи узлов с узлом 7. Прежний столбец матрицы Y для узла 5 войдет в систему уравнений умноженным на известное напряжение узла 5 – напряжение базисного узла.
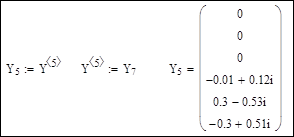
Матрица узловых проводимостей для нового расчета:
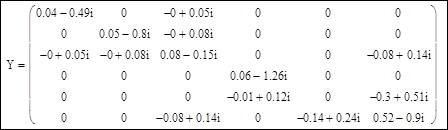
Матрица не является симметричной, и на диагонали имеется один нулевой элемент.
Напряжение нового базисного узла возьмем для сравнения результатов расчета таким, каким оно получилось в предыдущем расчете:
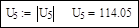
Решающий блок:
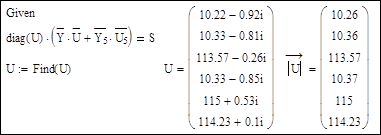
В векторе узловых напряжений на 5-м месте расположено значение напряжения в узле 7, которое являлось искомым и получилось именно таким, каким было задано в первом расчете. Все остальные напряжения совпадают с прежними значениями.
Дата добавления: 2015-03-19; просмотров: 2797;
