Нелинейные уравнения установившегося режима
Так как во многих случаях расчеты ведутся при заданных мощностях нагрузок и генерации, то их следует ввести в уравнения установившегося режима.
Мощность в трехфазной сети в симметричных режимах выражается суммарной мощностью всех трех фаз:
 (3.41)
(3.41)
В матричной форме это выражение можно записать, используя операцию диагонализации матрицы U. Матрица diag{U} есть квадратная матрица, в которой элементы матрицы U расположены по главной диагонали, а все остальные элементы равны нулю. Тогда
 (3.42)
(3.42)
Уравнение установившегося режима  записано для фазных токов и напряжений. Умножим обе части этого уравнения на
записано для фазных токов и напряжений. Умножим обе части этого уравнения на 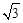 и применим к величинам этого уравнения операцию сопряжения, получим
и применим к величинам этого уравнения операцию сопряжения, получим
 (3.43)
(3.43)
В левой части этого уравнения после умножения на 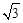 напряжения стали линейными.
напряжения стали линейными.
Умножим левую и правую части уравнения (3.43) слева на матрицу diag{U}, получим
 (3.44)
(3.44)
Система уравнений (3.44) является системой нелинейных уравнений установившегося режима. В зависимости от формы представления комплексных величин применяют две основные формы этой системы уравнений.
Вначале рассмотрим алгебраическую форму записи. Для i-го узла имеем:
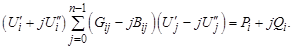 (3.45)
(3.45)
После перемножения двучленов и разделения уравнения на два уравнения с вещественными величинами получим систему 2(n – 1) алгебраических уравнений
 (3.46)
(3.46)
Здесь i = 1,…, n – 1.
Тригонометрическая форма нелинейных уравнений установившегося режима может быть получена, если комплексные величины в уравнении (3.44) записать в виде
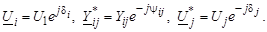 (3.47)
(3.47)
Тогда
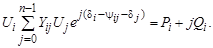 (3.48)
(3.48)
Уравнение (3.48) в тригонометрической форме запишется как
 , (3.49)
, (3.49)
 , (3.50)
, (3.50)
и после разделения на два вещественных уравнения
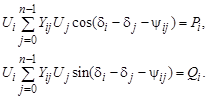 (3.51)
(3.51)
Обычно вместо угла yij используют дополняющий до 90° угол aij. aij = 90 - yij, yij = 90 - aij.
Тогда cos(di – dj – yij) = cos(di – dj – 90° + aij), а с учетом четности функции косинус cos(di – dj – 90°+ aij) = cos(90° – di + dj – aij). Имея
в виду, что cos(90° – b) = sin(b), получим cos(90° – di + dj – aij) =
= sin(di – dj + aij).
Аналогично sin(di – dj – yij) = sin(di – dj – 90 + aij) = –sin(90° – di +
+ dj – aij), в силу нечетности функции синус. Так как sin(90° – b) =
= cos(b), получим –sin(90° – di + dj – aij) = –cos(di – dj + aij). Подставляя полученные соотношения в (3.51), будем иметь:
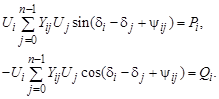 (3.52)
(3.52)
В полученной системе нелинейных уравнений установившегося режима искомыми переменными являются модули и фазовые углы напряжений, в то время как в уравнениях (3.46) неизвестными являются вещественная и мнимая составляющие напряжений.
Пример 3. Рассчитаем напряжения в узлах и потоки мощности в ветвях схемы сети, граф которой изображен на рис. 3.10. Исходные данные для расчета и расчет представлены в системе Mathcad.



Исходные данные
Погонные параметры ЛЭП:
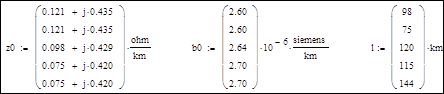
|
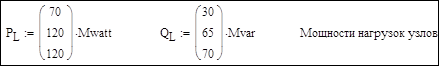

|

|

|

Модель электрической сети
1. Расчетные параметры ЛЭП:

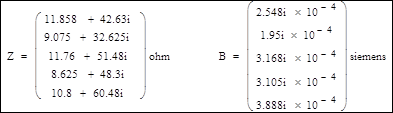
2. Составление матрицы инциденций узлов и ветвей M:

3. Формирование матрицы проводимостей ветвей Yb:

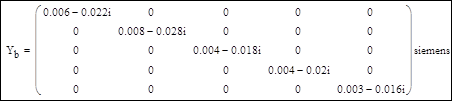
4. Получение матрицы узловых проводимостей Y:


5. Емкостные проводимости поперечных ветвей Yc:
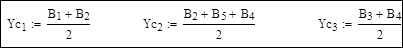
6. Корректировка диагональных элементов матрицы Y
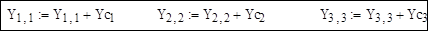
7. Расширение матрицы узловых проводимостей добавлением столбца для базисного балансирующего узла:


Вычисления
1. Решение системы нелинейных уравнений установившегося режима
Начальные приближения:

Решающий блок – приближенное решение:
|
|
|
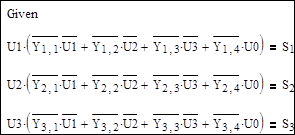
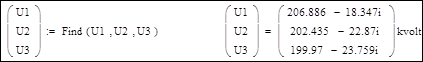
Результат решения – узловые напряжения (в экспоненциальной форме записи):

2. Расчет других параметров режима сети
Напряжения в начале и конце ветвей и токи узлов ветвей:

Мощности в начале и конце ветвей:
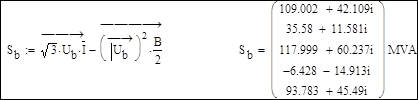

Потери мощности в ветвях:


3. Проверка результатов расчета: сумма мощностей узлов, потерь и зарядной мощности в сети должна быть равна мощности балансирующего узла:
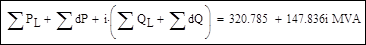
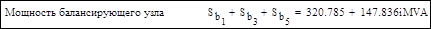
Дата добавления: 2015-03-19; просмотров: 1595;
