Формы линейных уравнений установившегося режима и их решение
Известными независимыми переменными в уравнениях установившегося режима могут быть задающие токи узлов и напряжение базисного узла. В этом случае решение уравнения (3.29) может быть записано в виде
 (3.30)
(3.30)
Здесь Z – матрица узловых сопротивлений.
Численное решение системы уравнений (3.29) выполняется методом Гаусса или другим методом решения системы линейных алгебраических уравнений.
В случае, когда известны мощности в узлах сети – задающие мощности Si, токи можно вычислить приближенно через номинальные напряжения  (i = 1,…, n – 1). Задающие мощности так же, как и токи, складываются из мощности генерации и мощности нагрузки:
(i = 1,…, n – 1). Задающие мощности так же, как и токи, складываются из мощности генерации и мощности нагрузки:
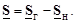 (3.31)
(3.31)
Другой приближенный подход связан с представлением задающих токов через напряжения и проводимости  , где YSi – проводимость генерации и/или нагрузки (схема замещения). Для i-го узла имеем:
, где YSi – проводимость генерации и/или нагрузки (схема замещения). Для i-го узла имеем:
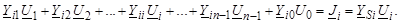 (3.32)
(3.32)
Объединив подобные члены, получим
 (3.33)
(3.33)
где в элемент Yii входит проводимость YSi. Знак перед этой проводимостью зависит от того, какая мощность преобладает в узле: плюс, если нагрузка, и минус, если генерация. В матричной форме записи:
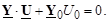 (3.34)
(3.34)
Решение матричного уравнения (3.34) запишется в виде
 (3.35)
(3.35)
Комплексную матрицу узловых проводимостей Y иногда представляют в блочной форме через ее вещественную G и мнимую B составляющие, и тогда система уравнений (3.34) становится системой с вещественными величинами:
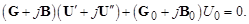 (3.36)
(3.36)
После перемножения двучленов в (3.35) будем иметь:
 (3.37)
(3.37)
Приравняем отдельно вещественные и мнимые части полученного уравнения и получим два матричных уравнения с вещественными величинами:
 (3.38)
(3.38)
или в компактной форме записи:
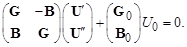 (3.39)
(3.39)
Решение (3.39) запишется в виде
 (3.40)
(3.40)
Пример 2.Рассчитаем напряжения в узлах и токи в ветвях схемы электрической сети, граф которой изображен на рис. 3.10. Исходные данные для расчета и расчет представлены в системе Mathcad.

Исходные данные
Напряжение базисного узла 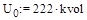
Сопротивления ветвей и задающие токи узлов:

Расчетные данные
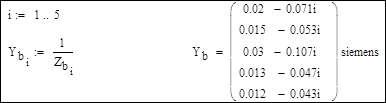
Модель электрической сети
1. Составление матрицы инциденций узлов и ветвей M:
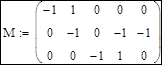
2. Формирование диагональной матрицы проводимостей ветвей Y:
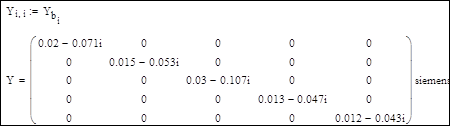
3. Составление матрицы-столбца проводимостей ветвей, связывающих узлы схемы с базисным узлом Y0:

4. Получение матрицы узловых проводимостей Y:

Вычисления
1. Решение системы линейных уравнений методом обратной матрицы:


2. Расчет других параметров режим сети:
|


3. Проверка результатов: сумма задающих токов должна быть равна току балансирующего узла с обратным знаком:
|
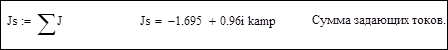
| |

Дата добавления: 2015-03-19; просмотров: 1863;
