Основы теории графов
Статические характеристики для каждого типа электрической нагрузки и их совокупностей могут быть получены экспериментально. Однако в каждом конкретном случае это затруднительно и чаще всего пользуются так называемыми типовыми характеристиками. Так, например, можно выделить статические характеристики асинхронных двигателей малой, средней и большой мощности или статические характеристики определенного состава смешанной нагрузки. Полученные по таким нагрузкам статические характеристики обобщаются и представляются в виде математических моделей. В общем случае статические характеристики нагрузки по напряжению могут быть представлены в виде
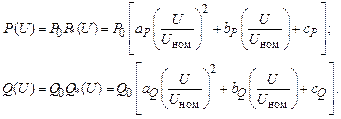
где P0 и Q0 – активная и реактивная мощности нагрузки при номинальном напряжении; P*(U) и Q*(U) – статические характеристики нагрузок в относительных единицах; Uном – номинальное напряжение нагрузки или сети; aP, aQ, bP, bQ, cP и cQ – коэффициенты (параметры) моделей, полученные в результате обработки экспериментальных данных.
Средние статические характеристики примерно соответствуют следующему составу нагрузки, %:
Крупные асинхронные двигатели..................................................... 15
Мелкие асинхронные двигатели........................................................ 35
Крупные синхронные двигатели....................................................... 9
Печи и ртутные выпрямители............................................................. 11
Освещение и бытовая нагрузка.......................................................... 22
Потери в сетях......................................................................................... 8
Обычно принимается aP = 0, т. е. линейная зависимость активной нагрузки от напряжения. Коэффициенты bP и cP в зависимости от характеристики узла нагрузки приведены в табл. 2.4.
Таблица 2.4
Значения коэффициентов bP и cP
| Характер нагрузки | Статические характеристики | |||||
| пологие | средние | крутые | ||||
| bP | cP | bP | cP | bP | cP | |
| Преобладают крупные промышленные предприятия | 0,3 | 0,7 | 0,6 | 0,4 | 0,9 | 0,1 |
| В среднем | 0,4 | 0,6 | 0,9 | 0,1 | 1,4 | –0,4 |
| Крупных промышленных предприятий нет | 0,9 | 0,1 | 1,2 | –0,2 | 1,5 | –0,5 |
Коэффициенты aQ, bQ и cQ в зависимости от коэффициента мощности приведены в табл. 2.5.
Таблица 2.5
Значения коэффициентов aQ, bQ и cQ
| Коэффициент мощности | Статические характеристики | ||||||||
| пологие | средние | крутые | |||||||
| aQ | bQ | cQ | aQ | bQ | cQ | aQ | bQ | cQ | |
| 0,83…0,87 | –18 | 9,6 | –15,3 | 6,7 | –14,4 | 5,4 | |||
| 0,88…0,90 | 11,9 | –21,8 | 10,9 | 11,4 | –18,5 | 8,1 | 11,9 | –17,4 | 6,5 |
| 0,91…0,93 | 14,1 | –26,2 | 13,1 | 13,5 | –22,2 | 9,7 | 14,1 | –21 | 7,9 |
Моделирование электрических нагрузок статическими характеристиками по напряжению в расчетах установившихся режимов считается наиболее точным способом учета потребляемой мощности нагрузки. Однако для получения действительных статических характеристик требуются экспериментальные исследования, а для подбора типовых статических характеристик должен быть известен состав нагрузки, который может сильно изменяться во времени. Кроме того, в этом случае в расчетах непременно следует учитывать действие регуляторов напряжения, что значительно усложняет подготовку данных и требует знания законов регулирования.
Поэтому в большинстве случаев пользуются самой простой моделью нагрузки – постоянными значениями активной и реактивной мощности: P = const, Q = const.
В некоторых задачах, в которых выполняются расчеты установившихся режимов, токов короткого замыкания в электрической сети или расчеты устойчивости ЭЭС, нагрузки принято представлять схемами замещения. Такое представление является точным в том случае, если для нагрузки известны ее статические характеристики и величина подведенного напряжения. В других случаях такие модели являются приближенными.
Рассмотрим электрическую цепь, в которой имеется нагрузка, представленная в виде сопротивления Zн. Это сопротивление в общем случае является переменной величиной – получается нелинейная электрическая цепь. Даже если считать мощность, потребляемую нагрузкой, постоянной, сопротивление будет меняться в зависимости от напряжения по формуле
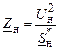 . (2.53)
. (2.53)
Кроме того, мощность также зависит от напряжения по статической характеристике и поэтому
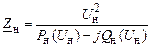 . (2.54)
. (2.54)
Нагрузка может быть представлена в виде двух схем замещения: с последовательным и параллельным соединением элементов (рис. 2.18).
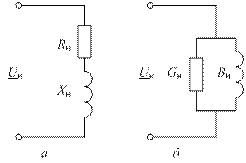
Рис. 2.18. Схемы замещения нагрузки
При последовательном соединении:
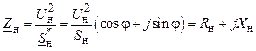 , (2.55)
, (2.55)
а при параллельном:
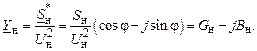 (2.56)
(2.56)
При постоянной величине заданного сопротивления или проводимости моделирование с помощью выражений (2.55) и (2.56) дает характеристики:
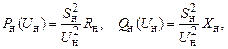
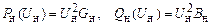 . (2.57)
. (2.57)
Моделирование постоянным сопротивлением дает обратную квад-ратичную зависимость от напряжения, а постоянной проводимостью – зависимость пропорционально квадрату напряжения. Вторая модель хорошо согласуется с моделью статической характеристики реактивной мощности нагрузки (2.52), поэтому для реактивной мощности вполне приемлема. Для активной мощности можно, например, воспользоваться линейной моделью, тогда будем иметь:
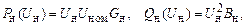 (2.58)
(2.58)
где Gн и Bн вычислены при номинальном напряжении нагрузки.
На рис. 2.19 представлены действительные статические характеристики нагрузки (сплошные линии) и характеристики, полученные по моделям (2.58) – пунктирные линии.
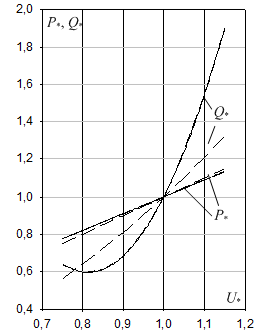
Рис. 2.19. Действительные статические характеристики нагрузки и зависимости мощностей от напряжения при модели-
ровании нагрузки схемой замещения
Иногда в качестве данных по нагрузке бывают известны измеренные токи нагрузки. Принимая какое-либо значение коэффициента мощности нагрузки, ее можно моделировать постоянными значениями токов Iн:
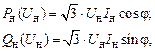 (2.59)
(2.59)
что дает линейные статические характеристики как активной, так и реактивной мощности. Такие модели нагрузки используются в низковольтных сетях и сетях среднего напряжения.
Все математические модели электрических нагрузок, рассмотренные выше, сведены в табл. 2.6.
Таблица 2.6
Математические модели электрических нагрузок
| Математические модели | Мощность нагрузки | Примечания |
| Статические характеристики нагрузки по напряжению | 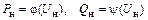
| Получаются по данным эксперимента или подбором типовых характеристик |
| Постоянные значения мощности нагрузки | 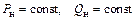
| |
| Схема замещения: Yн = Gн – jBн = = const | 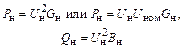
| 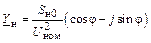
|
| Схема замещения: Zн = Rн + jXн = = const | 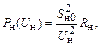
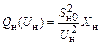
| 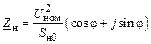
|
| Постоянное значение тока нагрузки: Iн = const (φ = const) | 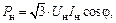
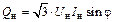
| 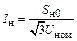
|
Примечание. Во всех формулах Sн0 – полная мощность нагрузки, которая может быть принята равной номинальной или максимальной мощности, а также мощности некоторого исходного или начального режима работы электроприемника или потребителя.
Пример.Найти коэффициенты статической характеристики нагрузки по опытным данным для активной и реактивной мощности и определить их регулирующие эффекты.
Используем линейную модель для активной мощности и параболу для реактивной мощности. Построение характеристик выполним в Mathcad.
Все величины приведены в относительных единицах.
Исходные данные (результаты эксперимента):
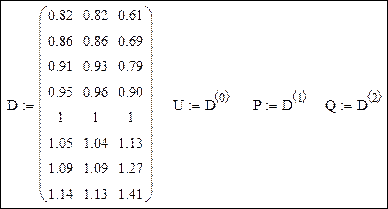
Коэффициенты функции полиномиальной регрессии:
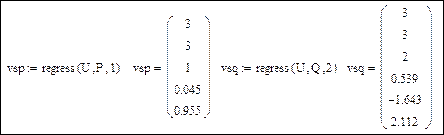
Определение функций статических характеристик и аргументов:
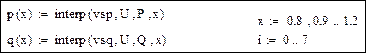
Графики статических характеристик (на графике отдельными маркерами нанесены экспериментальные данные):
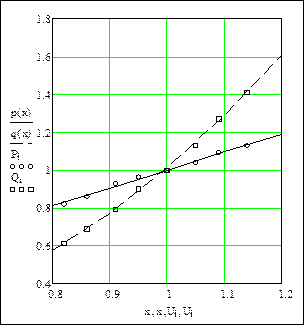
Регулирующие эффекты:
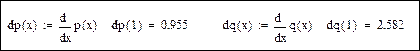
Изменение регулирующих эффектов:
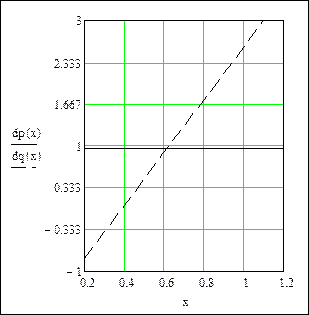
Регулирующий эффект активной мощности не меняется, так как модель статической характеристики была принята линейной.
Основы теории графов
Графы широко используются в различных областях науки и техники для моделирования отношений между объектами. На макроуровне графы применяются для графического изображения топологических уравнений.
Считается, что теория графов зародилась в XVIII столетии в г. Кенигсберге (ныне г. Калининград), жители которого пытались решить задачу о переходе мостов города (река Прегель) по такому маршруту, в котором бы были пройдены все мосты, но каждый мост был пройден только один раз (рис. 3.1, а). Эту задачу удалось решить Эйлеру. Он показал, каким условиям должен удовлетворять граф, полученный по схеме мостов, (рис. 3.1, б), чтобы такая задача имела решение.

Рис. 3.1. Схема мостов (а) и граф маршрутов (б)
Графом называется совокупность вершин (узлов) и связанных с ними ребер (ветвей). Граф можно задать в виде G = <V, E>, где V – множество вершин; E – отношение на V(E Ì V ´ V) – множество ребер. На рис. 3.2, а показан граф G, в котором множество ребер E есть {a, b, c, d, e, f, g}, а множество вершин V = {1, 2, 3, 4, 5}.
Подграфом называют такую часть графа, которая включает в себя некоторые вершины и ребра графа, причем среди ребер могут быть только те, которые связывают вершины подграфа. На рис. 3.2, б показан подграф G' графа G.
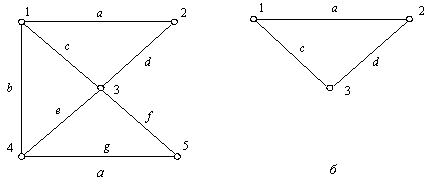
Рис. 3.2. Граф G (а) и его подграф G' (б)
Направленный (ориентированный) граф имеет ребра, на которых указаны направления. Ребра направленного графа называют дугами. На рис. 3.3, а показан ориентированный граф.

Рис. 3.3. Ориентированный граф (а), сечения дерева графа (б)
Степенью вершины Vi графа называют число ребер, инцидентных этой вершине. Термин «инцидентность» означает отношение объектов типа «проходят через…», «соединены с…». Две вершины называют смежными, если они соединены ребром. Например, на рис. 3.3, а вершина 4 смежна с вершиной 2, так как они соединены посредством ребра с.
Граничные вершины ребра – вершины, инцидентные этому ребру.
Кратные ребра – ребра с одинаковыми граничными вершинами.
Маршрутом (путем) S называют любую последовательность ребер, в которой соседние ребра инцидентны одной и той же вершине. В графе на рис. 3.2, а последовательности (a, d, e, g) и (b, g) – маршруты, а последовательность (d, g) маршрутом не является, так как ребра d и g инцидентны разным вершинам. Если в маршруте нет повторяющихся ребер, то он называется цепью. Если цепь начинается и кончается в одной и той же вершине, то она называется циклом-контуром. Количество ребер в S называют длиной маршрута.
Если каждому ребру графа приписано какое-то число (вес), то граф называют взвешенным.
Связным называют граф, в котором можно указать маршрут, связывающий любые вершины.
В задаче о кенигсбергских мостах (см. рис. 3.1) Эйлер показал, что такой граф не представляет собой единого цикла; иными словами, с какой бы вершины мы ни начали обход, мы не сможем обойти весь граф и вернуться обратно, не проходя никакого ребра дважды. Если бы такой цикл существовал, то, выйдя из начальной вершины, нужно было туда вернуться, а для всех промежуточных вершин нужно в них войти и выйти – степени всех вершин должны быть четными числами. Это условие не выполняется для кенигсбергских мостов.
Если на графе можно найти цикл, содержащий все его ребра, причем каждое ребро в точности по одному разу, то такой цикл называется эйлеровой линией, а граф, обладающий эйлеровой линией, – эйлеровым графом.
Если необходимо найти путь S в связанном графе, содержащий все его ребра по одному разу, в котором начальная и конечная вершины не совпадают, необходимо и достаточно, чтобы начальная и конечная вершины были единственными вершинами с нечетными степенями.
Деревом связного графа называют наименьший связный подграф данного графа.
Ветвями дерева называют ребра графа, вошедшие в дерево, а хордами – ребра графа, не вошедшие в дерево. Для одного и того же графа в общем случае можно указать несколько деревьев.
Контуром k-й хорды называют множество ребер, образующих цикл в графе, который получается при добавлении k-й хорды к дереву.
Сечением ветви дерева называют множество ребер, пересекаемых линией сечения, если:
а) среди ветвей дерева пересекается единственная;
б) линия сечения замкнутая и любое ребро может пересекаться не более одного раза.
Для графа, показанного на рис. 3.3, б, сечения ветвей его дерева записываются: a – (a, e); b – (b, d, e); c – (c, d, e).
Графы можно представить с помощью различных матриц, что является удобным при использовании алгебраических методов решения многих задач теории графов. Наиболее важными матричными представлениями являются матрицы инциденций (соединений) и смежности.
Первая матрица инциденций M для неориентированного графа представляет собой матрицу, строки которой соответствуют вершинам, а столбцы – ребрам. Элемент матрицы равен единице, если вершина инцидентна ребру. В противном случае элемент матрицы принимает значение ноль.
Для ориентированного графа элемент матрицы инциденций M равен +1, если вершина, инцидентная дуге, является начальной вершиной дуги (т. е. дуга исходит из этой вершины). Элемент равен –1, когда дуга входит в вершину. Если вершина не инцидентна дуге, то элемент матрицы равен 0. Так, для графа на рис. 3.3, а матрица M имеет следующий вид:
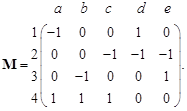 (3.1)
(3.1)
В каждом столбце матрицы M находится две единицы – одна положительная, а другая отрицательная, так как каждое ребро инцидентно только двум вершинам. В каждой строке имеется столько единиц, сколько ребер инцидентно соответствующей вершине.
Вторая матрица инциденций N устанавливает соответствие между ребрами графа и независимыми контурами графа. В зависимости от выбранной системы независимых контуров – дерева графа можно составить разные матрицы N. Число независимых контуров обозначают через k. Каждой строке матрицы N ставят в соответствие контур, таким образом, число строк в матрице N равно числу независимых контуров k; каждому столбцу матрицы N ставят в соответствие ребро, и число столбцов матрицы N равно числу ребер – m.
Матрица N составляется по следующим правилам. Независимые контуры нумеруют от 1до k; выбирают направления обхода контуров; начиная с первого выполняют обход контуров в соответствии с выбранными направлениями; проверяют, совпадает ли направление очередного ребра с направлением обхода контура: если да, то в соответствующем столбце матрицы N ставится +1, в противном случае –1; для ребер, не вошедших в рассматриваемый контур, в соответствующие столбцы проставляют нули.
Так, если в качестве дерева графа на рис. 3.3, а взять подграф с ребрами (a, b, c), то при добавлении хорды d образуется контур (a, d, c), а при добавлении хорды e – контур (c, e, b). Для такой системы независимых контуров матрица N имеет вид:
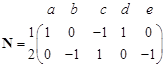 . (3.2)
. (3.2)
Матрица смежности A является квадратной матрицей и для невзвешенного графа состоит из нулей и единиц: Ai,j = 1, если (i, j ) Î E, и Ai,j = 0 в противном случае. Для взвешенного графа Ai,j равно весу соответствующего ребра, а отсутствие ребра в ряде задач удобно обозначать бесконечностью. Если граф ориентированный, то для каждого ребра ставится Ai,j = 1, если направление от i к j, а Aj,i = – 1 и наоборот. Для неориентированных графов матрица смежности всегда симметрична относительно главной диагонали. Для графа на рис 2.14, а матрица A имеет следующий вид:
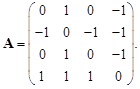 (3.3)
(3.3)
С помощью матриц M и A легко проверить, существует ли в графе ребро, соединяющее вершину i с вершиной j. Основной недостаток этих матриц заключается в том, что они требуют, чтобы объем памяти был достаточен для хранения соответственно nm и n2 значений.
Этого недостатка лишены такие способы хранения графа, как одномерный массив длины n списков или множеств вершин. В таком массиве каждый элемент соответствует одной из вершин и содержит список или множество вершин, смежных с ней.
Для реализации некоторых алгоритмов более удобным является описание графа перечислением его ребер. В этом случае его можно хранить в двумерном массиве из двух строк и длиной m, каждый столбец которого содержит номер начальной вершины и номер конечной вершины графа.
При работе с графами на компьютере удобно вершины графа сопоставлять с числами от 1 до n, где n = |V| – количество вершин графа, и рассматривать V = {1, 2, … n}. Ребра нумеруют числами от 1 до m, где m = |E|. В дальнейшем ребра будем именовать не буквами, а цифрами.
Дата добавления: 2015-03-19; просмотров: 1539;
