Математические модели на микроуровне. Рассмотрим модели технических систем на микроуровне

Рассмотрим модели технических систем на микроуровне. В большинстве случаев это распределенные модели (объекты с распределенными параметрами) и они представляют собой системы дифференциальных уравнений в частных производных. При создании математических моделей целесообразно исходить из основных физических законов в их наиболее «чистом», фундаментальном виде. Такой подход обеспечивает наиболее адекватное описание объектов, протекания процессов и явлений окружающего нас мира.

Фундаментальными физическими законами в первую очередь являются законы сохранения массы, количества движения, энергии. Эти законы можно сформулировать в одном общем виде: изменение во времени некоторой субстанции в элементарном объеме равно сумме притока-стока этой субстанции через поверхность элементарного объема. Субстанцией служат масса, количество движения, энергия. Эта формулировка остается справедливой и для некоторых других субстанций, например, количества теплоты, количества зарядов, количества элементарных частиц и др. Если внутри элементарного объема происходит генерация или уничтожение рассматриваемой субстанции, то к сумме притока-стока нужно добавить соответствующий член, отражающий данное явление. В этом случае общий вид уравнений, составляющих основу большинства распределенных моделей, будет следующим:

,

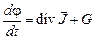где φ – некоторая фазовая переменная, выражающая субстанцию (плотность, энергию и т. п.);

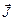– поток фазовой переменной;

G – скорость генерации субстанции;

t – время.

Поток фазовой переменной φ есть вектор 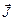= (J_x, J_y, J_z). Дивергенция (расходимость) этого вектора определяется общим соотношением

,

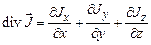является скалярной величиной и характеризует сумму притока-стока через поверхность элементарного объема.

Рассмотрим основные уравнения некоторых физических процессов.