Равновесие твердого тела при наличии трения качения
Если рассматриваемое тело имеет форму катка и под действием приложенных активных сил может катиться по поверхности другого тела, то из-за деформации поверхностей этих тел в месте соприкосновения могут возникнуть силы реакции, препятствующие не только скольжению, но и качению. Примерами таких катков являются различные колеса, как, например, у электровозов, вагонов, автомашин, шарики и ролики в шариковых и роликовых подшипниках и т.п.
Пусть цилиндрический каток находится на горизонтальной плоскости под действием активных сил. Соприкосновение катка с плоскостью из-за деформации фактически происходит не вдоль одной образующей, как в случае абсолютно твердых тел, а по некоторой площадке. Если активные силы приложены симметрично относительно среднего сечения катка, то есть вызывают одинаковые деформации вдоль всей его образующей, то можно изучать только одно среднее сечение катка. Этот случай рассмотрен ниже.
Между катком и плоскостью, на которой он покоится, возникают силы трения, если приложить к оси катка силу 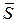 (рис. 7.5), стремящуюся его двигать по плоскости.
(рис. 7.5), стремящуюся его двигать по плоскости.
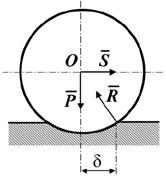
Рис. 7.5
Рассмотрим случай, когда сила 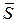 параллельна горизонтальной плоскости. Из опыта известно, что при изменении модуля силы
параллельна горизонтальной плоскости. Из опыта известно, что при изменении модуля силы 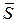 от нуля до некоторого предельного значения
от нуля до некоторого предельного значения 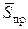 каток остается в покое, т.е. силы, действующие на каток, уравновешиваются. Кроме активных сил (веса
каток остается в покое, т.е. силы, действующие на каток, уравновешиваются. Кроме активных сил (веса 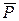 и силы
и силы 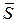 ), к катку, равновесие которого рассматривается, приложена реакция плоскости. Из условия равновесия трех непараллельных сил следует, что реакция плоскости
), к катку, равновесие которого рассматривается, приложена реакция плоскости. Из условия равновесия трех непараллельных сил следует, что реакция плоскости 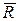 должна проходить через центр катка О, так как две другие силы приложены к этой точке.
должна проходить через центр катка О, так как две другие силы приложены к этой точке.
Следовательно, точка приложения реакции С должна быть смещена на некоторое расстояние 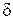 от вертикали, проходящей через центр колеса, иначе реакция
от вертикали, проходящей через центр колеса, иначе реакция 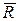 не будет иметь горизонтальной составляющей, необходимой для удовлетворения условий равновесия. Разложим реакцию плоскости
не будет иметь горизонтальной составляющей, необходимой для удовлетворения условий равновесия. Разложим реакцию плоскости 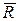 на две составляющие: нормальную составляющую
на две составляющие: нормальную составляющую 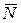 и касательную реакцию
и касательную реакцию 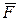 , являющуюся силой трения (рис. 7.6).
, являющуюся силой трения (рис. 7.6).
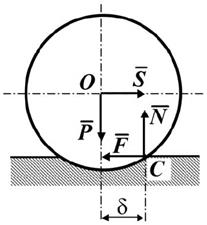
Рис. 7.6
В предельном положении равновесия катка к нему будут приложены две взаимно уравновешивающиеся пары: одна пара сил (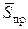 ,
, 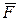 ) с моментом
) с моментом 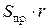 (где r – радиус катка) и вторая пара сил (
(где r – радиус катка) и вторая пара сил ( 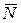 ,
, 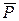 ), удерживающая каток в равновесии.
), удерживающая каток в равновесии.
Момент пары, называемой моментом трения качения, определяется формулой:
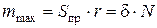 ,
,
из которой следует, что для того, чтобы имело место чистое качение (без скольжения), необходимо, чтобы сила трения качения 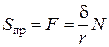 была меньше максимальной силы трения скольжения:
была меньше максимальной силы трения скольжения:
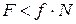 , ,
|
где f – коэффициент трения скольжения.
Таким образом, чистое качение (без скольжения) будет, если 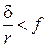 .
.
Трение качения возникает из-за деформации катка и плоскости, вследствие чего соприкосновение между катком и плоскостью происходит по некоторой поверхности, смещенной от нижней точки катка в сторону возможного движения.
Если сила 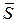 не направлена по горизонтали, то ее следует разложить на две составляющие, направленные по горизонтали и вертикали. Вертикальную составляющую следует сложить с силой
не направлена по горизонтали, то ее следует разложить на две составляющие, направленные по горизонтали и вертикали. Вертикальную составляющую следует сложить с силой 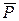 , и мы снова приходим к схеме действия сил, изображенных на рис. 7.6.
, и мы снова приходим к схеме действия сил, изображенных на рис. 7.6.
Установлены следующие приближенные законы для наибольшего момента пары сил, препятствующей качению:
1. Наибольший момент пары сил, препятствующий качению, в довольно широких пределах не зависит от радиуса катка.
2. Предельное значение момента 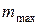 пропорционально нормальному давлению и равной ему нормальной реакции
пропорционально нормальному давлению и равной ему нормальной реакции 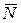 :
: 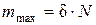 .
.
Коэффициент пропорциональности d называют коэффициентом трения качения при покое или коэффициентом трения второго рода. Коэффициент d имеет размерность длины.
3. Коэффициент трения качения d зависит от материала катка, плоскости и физического состояния их поверхностей. Коэффициент трения при качении в первом приближении можно считать не зависящим от угловой скорости качения катка и его скорости скольжения по плоскости. Для случая качения вагонного колеса по стальному рельсу коэффициент трения качения 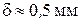 .
.
Законы трения качения, как и законы трения скольжения, справедливы для не очень больших нормальных давлений и не слишком легко деформирующихся материалов катка и плоскости.
Эти законы позволяют не рассматривать деформации катка и плоскости, считая их абсолютно твердыми телами, касающимися в одной точке. В этой точке соприкосновения кроме нормальной реакции и силы трения надо приложить еще и пару сил, препятствующую качению.
Для того, чтобы каток не скользил, необходимо выполнение условия
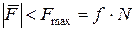 .
.
Для того чтобы каток не катился, должно выполняться условие
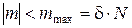 . .
|
Дата добавления: 2015-03-17; просмотров: 2462;
