По определению положения центров тяжести однородных тел
При решении задач на определение центра тяжести однородных тел сложной формы следует придерживаться следующего порядка:
1. Выбрать метод, который наиболее применим к данной задаче (метод разбиения или метод дополнения).
2. Разбить сложное тело на простые элементы, для которых центры тяжести известны.
3. Выбрать оси координат. При этом необходимо помнить, что: если тело имеет плоскость симметрии, то его центр тяжести лежит в этой плоскости; если тело имеет ось симметрии, то его центр тяжести лежит на этой оси; если тело имеет центр симметрии, то его центр тяжести совпадает с центром симметрии.
4. Определить координаты центров тяжести отдельных простых тел относительно выбранных осей.
5. Используя формулы, соответствующие выбранному методу, определить искомые координаты центра тяжести заданного тела.
6.6. Пример выполнения расчетно-графической работы по теме «Центр тяжести»
Пример. Определить центр тяжести однородной пластинки, изображенной на рис. 6.7.
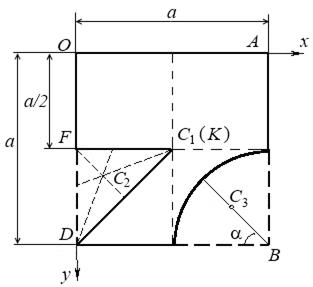
Рис. 6.7
Решение. Воспользуемся методом дополнения. Проведем через точку О пластинки оси Ох и Оу. Площадь данной пластинки представляет разность между площадью квадрата ОАBD и площадями прямоугольного треугольника и кругового сектора.
Площадь квадрата без вырезов: 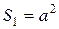 .
.
Абсцисса центра тяжести квадрата:  .
.
Рассмотрим треугольник DFK, центр тяжести которого находится в точке пересечения медиан. Очевидно, что  ~
~  .
.
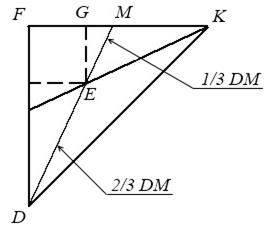
Рис. 6.8
|
 , а
, а  , то коэффициент подобия
, то коэффициент подобия  и
и 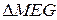 равен 1/3. Отсюда
равен 1/3. Отсюда 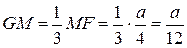 .
.
Тогда 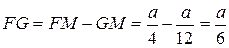 .
.
Таким образом  .
.
Площадь  равна:
равна: 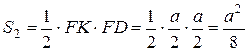 .
.
Определим координату центра тяжести и площадь кругового сектора.
Координата центра тяжести кругового сектора равна:
 , где
, где 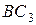 находим, используя данные табл. 6.1:
находим, используя данные табл. 6.1:
 , где
, где 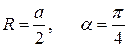 .
.
Тогда 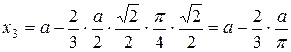 .
.
Площадь кругового сектора равна: 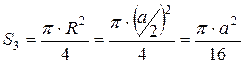 .
.
Тогда абсцисса центра тяжести пластинки будут равна:
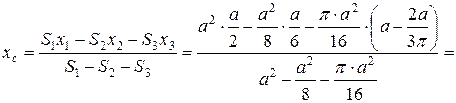
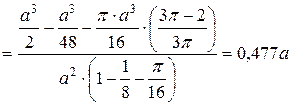 .
.
Аналогично находим ординату центра тяжести данной пластинки.
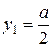 ;
; 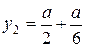 ;
;  .
.
Тогда:

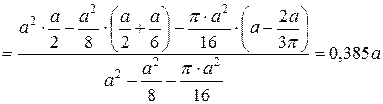 .
.
Ответ: 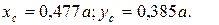
Дата добавления: 2015-03-17; просмотров: 1564;
