Механические колебания и волны. 4 страница

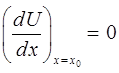
линейный по 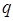член в выражении:

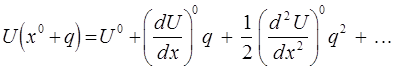
исчезает и с большей степенью точности:

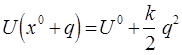
где

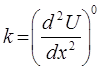
упругая постоянная связи (жёсткость пружины). В самом простейшем случае, совсем необязательно использовать потенциал 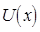сложной формы. Вместо потенциала вида:

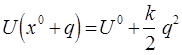
можно использовать универсальный потенциал с параболической зависимостью:

Такой подход оказывается достаточно удачным и при рассмотрении колебательных систем, в которых множество частиц образуют непрерывную колебательную среду. В данном случае величину 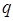заменяют разностью 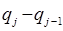соседних частиц. Потенциальную энергию такой многочастичной колебательной системы очевидно можно будет представить уравнением:

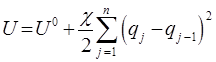
где 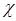– силовая постоянная. Поскольку на 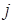-тую частицу в многочастичной колебательной системе действует некоторая сила :

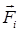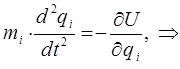
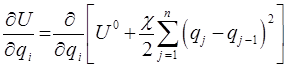
тогда:

и уравнения Ньютона приобретают вид:

где 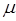– масса частицы (все частицы одинаковы). Вернёмся к нашей задаче. Так, по условиям данной задачи на интервале 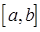находится большое число частиц, в пределе 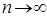, тогда:

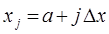
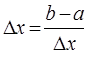
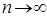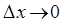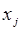Очевидно при , интервал между соседними частицами и будет принимать непрерывный ряд значений из 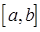. В то же время по 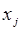воспроизводится индекс 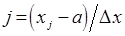. Тем самым устанавливается соответствие между дискретным номером 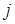и фактически непрерывным значением 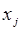из 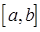. Тогда смещение 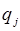для каждой 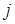-той частицы можно будет представить в виде некоторой функции 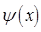, заданной на интервале 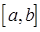и таким образом:

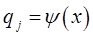
Введенную функцию 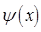, описывающую смещение частицы из положения равновесия и располагающейся в точке 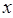, называют волновой функцией. Таким образом, волновая функция 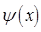характеризует величину смещения частицы из положения равновесия.

3.1.4.3. Волновой процесс.

Рассмотрим теперь более сложный случай – волновой процесс. Процесс распространения колебаний в сплошной среде, периодический во времени и пространстве, называется волновым процессом. При распространении волны, частицы среды не передвигаются вместе с волной, а колеблются около положений своих равновесий. При этом вместе с волной от частицы к частице среды передаётся лишь состояние колебательного движения и его энергия. Поэтому основным свойством всех волн, независимо от их природы – является перенос энергии в отсутствии переноса вещества. Можно выделить следующие типы волн: волны на поверхности жидкости, упругие (механические) волны и электромагнитные волны. Упругие волны бывают продольными и поперечными. Если частицы колеблются по той же прямой, вдоль которой распространяется колебание, то такая волна называется продольной; если колебания частиц перпендикулярны к направлению распространения колебаний, то волна называется поперечной. Таким образом, продольные волны могут распространяться лишь в том случае, если в среде возникают силы упругости при деформации сжатия и растяжения. Если же при сдвиге одного слоя среды по отношению к другому слою возникают упругие силы, стремящиеся возвратить сдвинутый слой в положение равновесия, то в среде могут распространяться поперечные волны. Если такие силы в среде не возникают, то поперечные волны образоваться не могут. Являются ли волны, распространяющиеся в среде, продольными или поперечными – зависит от упругих свойств среды. Расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, называется длиной волны . Длина волны равна тому расстоянию, на которое распространяется данная фаза колебания за период . Имеем соответственно:

учитывая, что:

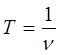
будем иметь соответственно:

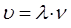
Две волны называют когерентными, если частицы колеблются в одинаковых фазах. Геометрическое место точек, до которых доходят колебания к моменту времени , называется волновым фронтом. Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью. Волновые поверхности могут быть любой формы. Если волновая поверхность представляет собой совокупность плоскостей, параллельных друг другу, то такая волна называется плоской. Если же волновая поверхность представляет совокупность концентрических сфер, параллельных друг другу, то такая волна будет называться сферической. Пусть в системе происходит волновой процесс и в точке находится начальная фаза колебаний 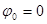(примем, что оно совершается по закону синуса). Для упрощения выкладок будем рассматривать плоскую волну, распространяющуюся вдоль одной из координатных осей (например, вдоль оси 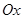) – одномерный случай, тогда будем иметь соответственно:

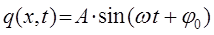
после подстановки начального условия 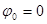, будем иметь:

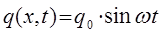
Возьмём на прямой 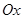произвольную точку М, лежащую от начала координат (точка ) на расстоянии . Очевидно, что колебания распространяясь от точки , дойдут до точки М через промежуток времени 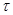. Тогда, следовательно:

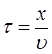
Таким образом, точка М начнёт колебаться на время 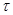позже точки , поэтому:

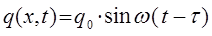
или с учётом соотношения вида:

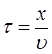
получим соответственно:

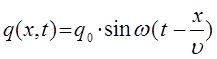
Полученное выше соотношение, представляет собой уравнение плоской волны, распространяющейся вдоль оси . Фронт такой волны будет представлять собой плоскость. Данное уравнение задаёт смещением 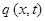как функцию времени и расстояния от точки М до центра колебаний лежащего в точке . Очевидно, что аргумент:

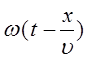
есть не что иное, как фаза волны 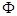. Если представить себе волну, распространяющуюся в направлении, обратном рассмотренному выше, тогда уравнение плоской бегущей волны вида:

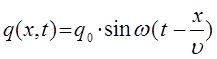
должно быть заменено уравнением вида:

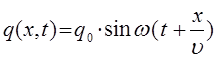
Полученные нами выше уравнения для двух взаимообратных плоских бегущих волн:

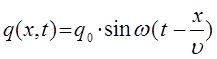
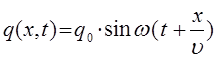
могут быть преобразованы далее к виду:

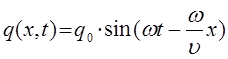
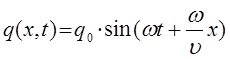
учитывая выражения вида:

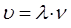
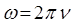
будем иметь соответственно:

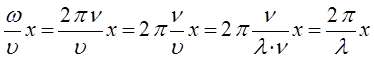
здесь величина вида:

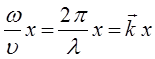
представляет собой волновой вектор. Тогда соответствующие уравнения для плоских бегущих волн можно представить к виду:

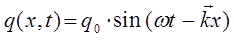
Для последующих выкладок удобней представить полученные выражения в экспоненциальной форме. При этом ограничимся рассмотрением лишь таких волн, которые распространяются вдоль оси 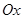в прямом направлении.

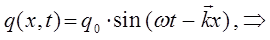
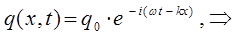
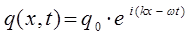
Уравнение де Бройля (для случая плоских волн), есть одно из возможных решений дифференциального уравнения в частных производных, описывающее процесс распространения возмущения (колебания) в среде. Такое уравнение называется волновым уравнением. Для его получения необходимо дважды продифференцировать полученное выше уравнение плоской бегущей волны по координате и дважды по времени , тогда:

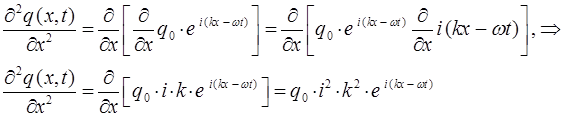
с учётом выражений вида:

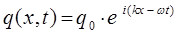
а также, что:

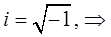
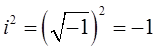
будем иметь соответственно:

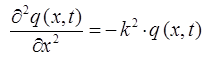
Аналогично получаем значение второй производной по времени:

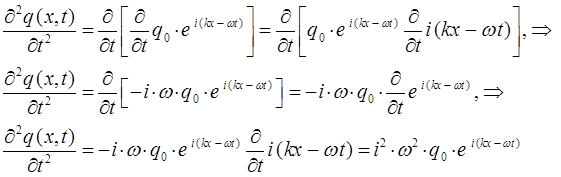
и таким образом будем иметь соответственно:

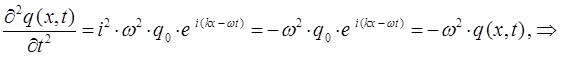
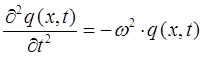
Таким образом, в ходе проделанных операций дифференцирования, мы пришли к выражениям вида:

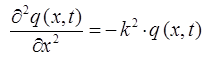
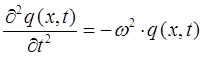
Выражая из полученных выражений величину 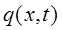и приравнивая между собой общую переменную 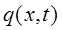, будем иметь соответственно:

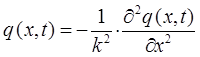
аналогично:

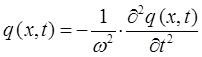
имеем таким образом:

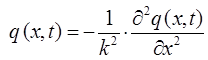
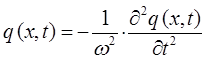
откуда следует, что:

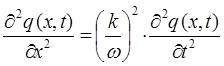
с учётом выражения вида:

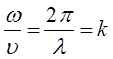
будем иметь соответственно:

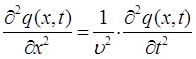
тогда соответственно:

Полученное нами выше волновое уравнение описывает распространение плоской бегущей волны вдоль оси . Однако оно остаётся справедливым и для трёхмерного случая. Распространяя данное уравнение для случая трёх пространственных координат, полученное выше волновое уравнение можно записать в так называемом обобщённом виде:

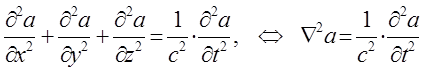
К выводу данного уравнения можно прийти и несколько другим способом. Так, в предыдущем разделе мы подробно рассмотрели многочастичные колебательные системы. При рассмотрении механических систем такого типа было получено уравнение, согласно которому, на колеблющуюся -тую частицу в непрерывной колебательной среде оказывается сила равная:

Для больших систему дифференциальных уравнений вида:

нетрудно преобразовать в одно дифференциальное уравнение для волновой функции 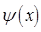, в частности:

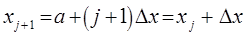
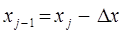
и малость при 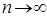. Это в свою очередь позволяет разложить в ряд Тейлора:

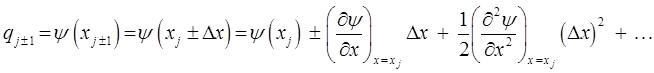
и представить:

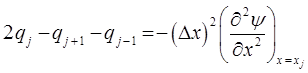
кроме того, аналогия:

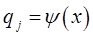
позволяет заменить также:

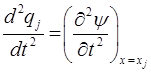
В результате из выражения:

получаем для всех 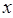из промежутка 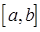уравнение:

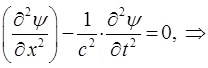
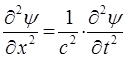
где величина 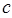– имеет размерность скорости и определяется выражением:

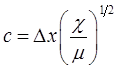
Полученное нами выше уравнение:

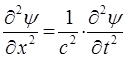
называется волновым, так как описывает распространение колебаний в непрерывных средах – волновой процесс. Данное уравнение легко обобщается на случай трёх пространственных координат, тогда соответственно:

Решением такого уравнения приводит к суперпозиции решений, комплексно сопряжённых друг другу. В этом случае образуется стоячая волна, состоящая из двух бегущих волн, каждая из которых движется на встречу друг другу. Стоячая волна является по существу не волной, а колебательным процессом, происходящим в среде или теле. Поэтому определение волна (в строгом смысле этого слова) – к стоячим волнам не относится. В реальной среде стоячая волна затухает в результате диссипации (рассеяния) энергии. Для поддержания стоячих волн, необходима их подпитка бегущей волной. В стоячей волне все точки среды колеблются с разными амплитудами, а фазы колебаний точек по разную сторону от узла – противоположны, отличаясь на величину 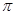. В бегущей волне все точки среды колеблются с одинаковой амплитудой, одновременно в разных фазах. В стоячей волне, в отличие от бегущей, нет переноса энергии. В ней происходит периодическое превращение одного вида энергии в другой – например, кинетической энергии в потенциальную и наоборот. Это обусловлено тем, что стоячая волна сформирована двумя бегущими волнами, распространяющимися и переносящими энергию в противоположных направлениях.