Статистического наблюдения
В результате статистической обработки материалов исследований получают обобщающие величины, характеризующие совокупность в целом – относительные показатели (коэффициенты) и средние величины. Если эти величины получены на достаточно большом и качественно однородном материале, т.е. если выборка была репрезентативной (представительной), то их можно считать достаточно точными для характеристики изучаемого явления.
Получив результат (среднюю величину или показатель), мы считаем его характеристикой изучаемого явления. Точность этой характеристики зависит от числа наблюдений. Чем больше число наблюдений, тем точнее результат. Чем меньше число наблюдений, тем результат хуже отражает изучаемое явление, тем он больше отличается от того результата, который мог бы быть получен на генеральной совокупности (т.е. из всех единиц наблюдения изучаемого явления).
Различие результатов выборочного исследования и результатов генеральной совокупности представляет собой ошибку выборочного исследования. Ошибка средней величины или показателя может быть определена математическим путем и оценена.
Средняя ошибка показателя рассчитывается по формуле:
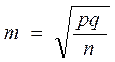 , где
, где
m – средняя ошибка показателя,
p – величина показателя (в долях единицы, процентах или про- милях),
q – (1 – p) или (100 – p) или (1000 – p) в зависимости от единиц
измерения показателя p,
n – число наблюдений.
Пример 7. При изучении заболеваемости болезнями щитовидной железы (гипотиреозом) на территории с техногенным загрязнением почвы Ј131 обследовано 400 человек. Гипотиреоз выявлен у 37 человек (9,3 %). Рассчитаем ошибку исследования:
m = 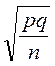 ; m=
; m=  .
.
Средняя ошибка средней рассчитывается по формуле:
 , где
, где
δ – среднее квадратическое отклонение,
n – число наблюдений.
Пример 8. Средняя температура воды в водоеме при ежедневном измерении (30 измерений) в июне 2010г.составила 20ºС при δ = ± 2,1. Рассчитаем ошибку исследования:
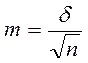 ;
; 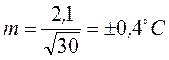 .
.
Средняя ошибка показателя или средней величины служит для определения пределов их случайных колебаний, т.е. она дает представление, в каких пределах может находиться показатель в различных выборках генеральной совокупности в зависимости от различных случайных причин.
Для оценки полученного показателя или средней величины в соответствии с их средней ошибкой необходимо определить интервал и его границы, в которых может находиться истинное значение показателя, а также надежность этого предположения.
Интервал, в котором с заданным уровнем вероятности находится истинное значение показателя или средней величины, называется доверительным интервалом, а его границы – доверительными границами.
Надежность – вероятность того, что ошибка полученного показателя будет не больше определенной величины.
Теория вероятности устанавливает, что с вероятностью, равной 68 %, пределы колебаний показателя будут находиться в интервале ± m, с вероятностью 95 % – в интервале ± 2m и 99,7 % – в интервале ± 3m.
Пример оценки достоверности показателя (пример 9).
Заболеваемость болезнями щитовидной железы (гипотиреозом) на территории с техногенным загрязнением почвы Ј131 равна 9,3 %, m = 1,5 %. При условии увеличения числа наблюдений этот показатель может измениться. Величина этого изменения связана с ошибкой исследования, т.е. он может быть равен 9,3 ± 1,5 %. Однако, вероятность того, что этот показатель будет находиться в пределах от 7,8 до 10,8 % довольно мала (68 %). С большей степенью вероятности (95 % шансов) можно утверждать, что показатель будет находиться в пределах ± 2m, т.е. от 6,3 до 12,3 %. И, наконец, наиболее точное суждение (99,7 % вероятности), что показатель расположится в пределах ± 3m, т.е. от 4,8 до 13,8 %.
Сам исследователь должен решить, насколько приемлемы для него подобные доверительные границы, а отсюда, достаточно ли наблюдений для данного исследования.
В практической работе чаще всего приходится встречаться с необходимостью оценивать достоверность различий между показателями, полученными в динамике или при исследовании разных групп наблюдения.
Мерилом достоверности разности показателей является ошибка этой разности, которая определяется по формуле:
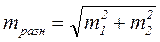 , где
, где
mразн. – средняя ошибка разности,
m1 – средняя ошибка первого показателя (или средней величины),
m2 – средняя ошибка второго показателя (или средней величины).
Различия между показателями считаются достоверными, (с 95% надежностью), если разность показателей будет превышать более, чем в 2 раза свою ошибку (среднюю ошибку разности). Отношение разности показателей к средней ошибке разности называется коэффициентом достоверности:

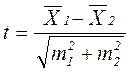 .
.
(для показателей) (для средних величин)
При t 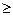 2 различия не случайны, существенны, достоверны. При t < 2 различия случайны, недостоверны.
2 различия не случайны, существенны, достоверны. При t < 2 различия случайны, недостоверны.
Приведем два примера оценки различий показателей.
Пример 10. При изучении заболеваемости болезнями щитовидной железы (гипотиреозом) на территории с техногенным загрязнением почвы J131 обследовано 400 человек. Контрольную группу составили 400 жителей территории, не подвергавшейся техногенному загрязнению J131. В основной группе гипотиреоз выявлен у 37 обследованных (p = 9,3 %), в контрольной – у 14 человек (p = 3,5 %).
Ошибка исследования
m = 
в первом случае составила
m1 = 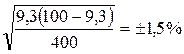 ,
,
во втором случае
m2=  .
.
Коэффициент достоверности различий
t =  cоставил t =
cоставил t =  .
.
Разность показателей в 3,4 раза превышает ошибку разности, следовательно, различие между показателями неслучайно.
Пример 11. Средняя температура воды в водоеме в июне 2010г. составляла 20º, m=±0,4º. Весной 2011г. в водоем стала поступать вода из охлаждающего пруда ТЭС. В июне 2011г. температура воды в водоеме составила 22º, m=±0,3º. Коэффициент достоверности различий
 составил
составил 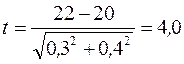 .
.
Разность средних значений в 4 раза превышает ошибку разности. Следовательно, различие между средними значениями температуры воды в июне 2010г. и 2011г. неслучайно.
Если разность оказывается недостоверной, не следует утверждать, что различия отсутствуют. Нам не удалось статистически доказать существенность различий из-за недостаточного числа наблюдений.
При малом числе наблюдений вформулу вычисления средней ошибки вводится дополнение: в знаменателе берется не число наблюдений, а n – 1. Малым числом наблюдений считаются группы с числом наблюдений меньше 30 случаев. При оценке достоверности различий в группах с малым числом наблюдений пользуются специальной таблицей (Стьюдента) (табл. 3).
Пример 12. По результатам исследования воды в реке (4 раза в месяц в течение 3х летних месяцев, всего 12 проб) в точке отбора № 1 средняя концентрация хрома Cr+6 равнялась 26 мкг/л, минимальная концентрация составила 20 мкг/л, максимальная –
Таблица 3.
Таблица значений t (Стьюдента) при малой выборке
| число степеней свободы (n´´) | вероятность ошибки (Р) | ||
| 0,05 = 5 % | 0,01 = 1 % | 0,001 = 0,1 % | |
| 12,71 | 63,66 | 636,62 | |
| 4,30 | 9,93 | 31,60 | |
| 3,18 | 5,84 | 12,94 | |
| 2,78 | 4,60 | 8,61 | |
| 2,57 | 4,03 | 6,86 | |
| 2,45 | 3,70 | 5,96 | |
| 2,37 | 3,50 | 5,40 | |
| 2,30 | 3,36 | 5,04 | |
| 2,26 | 3,25 | 4,78 | |
| 2,23 | 3,17 | 4,59 | |
| 2,20 | 3,11 | 4,49 | |
| 2,18 | 3,06 | 4,32 | |
| 2,16 | 3,01 | 4,22 | |
| 2,14 | 2,98 | 4,14 | |
| 2,13 | 2,95 | 4,07 | |
| 2,12 | 2,92 | 4,02 | |
| 2,11 | 2,90 | 3,97 | |
| 2,10 | 2,88 | 3,92 | |
| 2,09 | 2,86 | 3,88 | |
| 2,09 | 2,85 | 3,85 | |
| 2,08 | 2,83 | 3,82 | |
| 2,07 | 2,82 | 3,79 | |
| 2,07 | 2,81 | 3,78 | |
| 2,06 | 2,80 | 3,75 | |
| 2,06 | 2,79 | 3,72 | |
| 2,06 | 2,78 | 3,71 | |
| 2,05 | 2,77 | 3,69 | |
| 2,05 | 2,76 | 3,67 | |
| 2,04 | 2,76 | 3,66 | |
| 2,04 | 2,75 | 3,65 | |
| ∞ | 1,96 | 2,58 | 3,29 |
Примечание: n´ = n1 + n2 – 2
33 мкг/л; в точке отбора № 2 средняя концентрация составила 34 мкг/л, минимальная концентрация – 20 мкг/л, максимальная – 44 мкг/л.
Рассчитаем параметры вариационных рядов.
В точке отбора № 1:
 = 26 мкг/л;
= 26 мкг/л;
δ =  ; δ1 =
; δ1 = 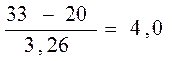 мкг/л;
мкг/л;
 ;
; 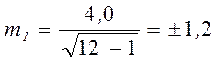 мкг/л.
мкг/л.
В точке отбора № 2:
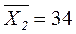 мкг/л; δ2 =
мкг/л; δ2 = 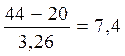 мкг/л;
мкг/л;
m2=  мкг/л.
мкг/л.
Коэффициент достоверности различий средних концентраций хрома в точках отбора воды в реке № 1 и № 2
 составит
составит 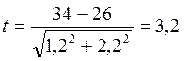 .
.
Пользуясь табл.3, с учетом числа степеней свободы n´=22 определяем, что разность полученных значений неслучайна (с вероятностью ошибки 1 %).
Дата добавления: 2014-12-16; просмотров: 1724;
