Средние величины

В начале раздела 1.2. было указано, что статистические характеристики объекта эпидемиологического исследования могут быть представлены в виде абсолютных чисел или обобщающих величин, к числу которых принадлежат относительные числа (коэффициенты, показатели) и средние величины. Если относительные числа служат обобщающей характеристикой качественных признаков объекта наблюдения, то средние величины выступают в качестве обобщающей характеристики его количественных признаков.

В процессе наблюдения за явлением, характеризующимся по количественному признаку, мы получаем отдельные значения признака каждого случая наблюдения − варианты, например, длительность нетрудоспособности каждого больного определенной болезнью, количество эритроцитов в крови каждого обследованного человека, концентрация определенного вещества в каждой пробе определенного объекта окружающей среды, значение физического фактора среды при каждом измерении.

Совокупность вариант, расположенных в порядке нарастания их величины, составляет вариационный ряд. Обработка вариационного ряда заключается в выявлении его параметров: средней величины, среднего квадратического отклонения и средней ошибки средней величины.

Средняя величина − это величина, характеризующая одним числом всю совокупность в целом.

В простом вариационном ряду, где каждая варианта встречается лишь один раз (частоты равны единице), средняя (арифметическая) получается простым суммированием отдельных вариант и делением суммы на их общее число (число наблюдений).

В тех рядах, где число наблюдений больше 30, и варианты сгруппированы, вычисляют взвешенную среднюю арифметическую. Формула ее вычисления:

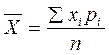_, где

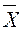– средняя арифметическая взвешенная,

х_i – значения отдельных вариант,

р_i – частоты этих вариант.

В некоторых случаях средние величины могут быть представлены не в виде средних арифметических, а в форме средних геометрических или средних гармонических. Средняя геометрическая вычисляется тогда, когда изменение членов статистического ряда происходит в соответствии с геометрической прогрессией. Средняя гармоническая вычисляется в том случае, если вариационный ряд представлен дробями, т.е. варианты ряда находятся в знаменателе. В большинстве же случаев под средней величиной понимается именно средняя арифметическая.

Средние являются важными характеристиками совокупности. Однако за ними скрываются индивидуальные значения признака. Средние величины не показывают изменчивости, колеблемости признака, его рассеянности.

Естественно, если вариационный ряд более компактен, менее рассеян, и все отдельные значения расположены вокруг средней, то средняя величина лучше характеризует данную совокупность. Если вариационный ряд растянут, отдельные значения признака существенно отклоняются от средней величины, т.е. имеет место большая вариабельность признака, то средняя менее типична, хуже отражает свой ряд. Следовательно, кроме средней величины необходима вторая характеристика ряда – степень его колеблемости.

Простейшей мерой рассеянности является вариационный размах – амплитуда колебания, т.е. разность крайних значений ряда (х_max – х_min).

Пример 4. При исследовании проб воды в реке (4 раза в месяц в течение 3^х летних месяцев) в точке отбора № 1 средняя концентрация хрома равнялась 30 мкг/л, минимальная концентрация составила 24 мкг/л, максимальная концентрация – 37 мкг/л. В точке отбора № 2 средняя концентрация хрома в воде также была равна 30 мкг/л, но минимальная концентрация составила 16 мкг/л, а максимальная – 42 мкг/л. В пробах воды из точки отбора № 1 амплитуда концентраций хрома значительно меньше, и, следовательно, все значения группируются вокруг средней. Вторая совокупность более разнообразна, ее рассеянность велика, отклонения отдельных значений концентраций металла от средней больше.

Чаще всего в качестве мерила изменчивости, колеблемости признака используется среднее квадратическое отклонение (δ). Чем больше среднее квадратическое отклонение, тем степень колеблемости данного ряда выше.

Методика получения среднего квадратического отклонения такова:

1) Находят среднюю арифметическую величину ( ).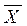

2) Определяют отклонения отдельных вариант от средней

арифметической (х_i – 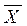). Так как сумма всех отклонений

равняется нулю, то для получения общей величины откло -

нений производят дальнейшие вычисления.

3) Возводят отклонение в квадрат с тем, чтобы избавиться от отрицательных значений отклонений и увеличить значения крайних отклонений: (х_i – 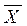)².

4) Перемножают квадраты отклонений на соответствующие частоты : (х_i – 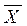)² p.

5) Вычисляют среднее квадратическое отклонение по формуле:

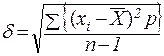, где

n – число всех вариант.

Рассмотрим получение среднего квадратического отклонения на примере 5 (таблица 1).

Таблица 1.