Выборочного статистического наблюдения

Репрезентативность (представительность) выборки по отношению к генеральной (общей) совокупности достигается за счет двух моментов.

Первый момент, обеспечивающий репрезентативность выборочного исследования – качественный. Это как можно более точное соответствие соотношения отдельных частей в выборочной совокупности соотношению частей во всей совокупности в целом. При этом репрезентативность достигается за счет правильного отбора единиц наблюдения в выборочную совокупность. Важно, чтобы любая единица всей совокупности в целом имела равновеликую возможность попасть в выборочную совокупность. В то же время выборочная совокупность должна по качественной характеристике быть как возможно ближе ко всей (генеральной) совокупности.

Качественная характеристика репрезентативности статистической выборки достигается использованием нескольких способов отбора единиц наблюдения.

Первый способ репрезентативного отбора единиц наблюдения в выборку – это организация типологической выборки. Она предполагает разбивку изучаемой совокупности на ряд однотипных качественных групп, из которых далее отбираются единицы для наблюдения. Например, при изучении онкологической заболеваемости населения в зоне влияния промышленного объекта, выступающего в качестве источника поступления в окружающую среду канцерогенных веществ, все население этой зоны, как генеральная совокупность, разбивается на группы в соответствии с проживанием в зонах различного радиуса от источника. Затем из каждой группы отбирается одинаковая доля (процент) единиц наблюдения (проживающих в каждой зоне людей). Все вместе они и составят выборочную совокупность.

Второй способ отбора – случайный (наудачу, по жребию, по начальной букве фамилии или дню рождения, по таблице случайных чисел (приложение 1)).

Третий способ отбора – механический, когда из всей (генеральной) совокупности берется для изучения механически отобранная пятая (20 %) или десятая (10 %) часть. Например, при изучении заболеваемости болезнями щитовидной железы на определенной территории в разработку берется механически каждая пятая (каждая десятая) карта амбулаторного больного с соответствующим диагнозом.

Четвертый способ отбора – «гнездовой», когда из всей совокупности отбираются группы, называемые гнездами. Затем в этих гнездах единицы наблюдения изучаются сплошь или выборочно (механическим или случайным отбором). Например, для представления о заболеваемости детей кариесом на территории с пониженным содержанием фтора в воде изучают заболеваемость детей одного населенного пункта, наиболее типичного для данной территории.

Пятый способ отбора – направленный. Использование принципов направленного отбора позволяет выявить влияние неизвестных факторов при устранении влияния известных. Например, при изучении влияния степени дефицита фтора в воде на заболеваемость населения кариесом на территориях с различным содержанием фтора в воде для исследования отбираются люди одного возраста с одинаковым уровнем доходов, с одинаковым уровнем образования, с одинаковым уровнем обеспечения стоматологической помощью.

Второй момент, обеспечивающий репрезентативность выборочного исследования – количественный. Объем выборки (численность единиц в выборке) должен быть достаточным для обеспечения достоверности и надежности результатов в отношении генеральной совокупности.

В том случае, когда статистическому исследованию подлежат качественные признаки (например, наличие болезни или смерти), при расчете необходимого объема выборки используется формула определения предельной ошибки показателя.

Непременным условием обоснованного расчета необходимого числа наблюдений в статистическом исследовании является допущение возможной ошибки, т.е. предположение максимально допустимого отклонения результатов выборочного исследования от значений генеральной совокупности. Например (пример 13), при изучении заболеваемости болезнями щитовидной железы (гипотиреозом) на территории с техногенным загрязнением почвы J¹³¹ мы ожидаем получить результат 10 %. Какую ошибку можно допустить, т.е. в каких пределах можно разрешить колебаться средней величине показателя, чтобы не исказить результаты? Определим эту предельную ошибку в 3 %, т.е. истинный показатель заболеваемости будет находиться в доверительных границах 10 ± 3 % или от 7 до 13 %. Итак, предельная ошибка (∆) будет равна 3 %, величина самого показателя (р) − 10 %.

Математическая статистика предлагает формулу для определения предельной ошибки показателя:

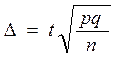,где

∆ − предельная ошибка показателя;

р − величина показателя (для изучаемого признака);

q − (1– р) или (100 – р) в зависимости от того в каких величинах выражается показатель (в долях единицы или в процентах);

n − число наблюдений;

t − коэффициент, показывающий с какой вероятностью (надежностью) можно гарантировать, что действительные размеры показателя не будут выходить за границы предельной ошибки (обычно t берется равным 2, что обеспечивает высокую степень достоверности будущего результата).

Исходя из формулы предельной ошибки, можно вывести

формулу необходимого числа наблюдений:

.

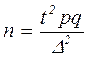В нашем примере:

∆ = 3 %; р = 10 %; q = 100 % – 10 % = 90 %; t = 2.

Пользуясь выведенной формулой, вычисляем необходимое число наблюдений:

.

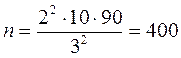Полученный результат свидетельствует, что при изучении заболеваемости болезнями щитовидной железы на территории с повышенным содержанием радиоактивного йода достаточно проанализировать результаты обследования 400 человек. Результаты их обследования будут репрезентативно отражать состояние всей совокупности. При отборе этих 400 человек должен быть использован один из пяти описанных выше способов, обеспечивающих качественную репрезентативность выборки.

В том случае, когда изучению подлежат количественные признаки (показатели физического развития, длительность заболевания, содержание веществ в крови, тканях, воздухе, воде, почве и т.д.) при расчете необходимого числа наблюдений применяют формулу предельной ошибки средней величины:

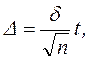откуда 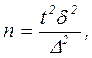где

δ − среднее квадратическое отклонение.

Для расчета объема выборки в этом случае следует знать вариабельность признака (δ) из предыдущих исследований или путем пробных выборок, а также определить возможную ошибку, которую можно допустить в исследовании (∆).

Например (пример 14), нас интересует содержание 3,4-бенз -пирена в атмосферном воздухе на территории города. По результатам предыдущих исследований среднеквадратическое отклонение его средней концентрации (δ) составляло 0,4 нг/м³. Ошибка, которая может быть допущена, равна 0,1 нг/м³. В таком случае необходимое число проб воздуха на содержание 3,4-бензпирена

составит:

n = 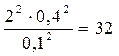пробы.

<14 15 161718 19 20 >

Дата добавления: 2014-12-16; просмотров: 1310;