Математические модели процесса получения хлорноватистой кислоты.
Используя методологию амбивалентных систем, как систем с противоположностями, были получены различные математические модели процесса получения хлорноватистой кислоты. В качестве примера приведем математическую модель процесса получения хлорноватистой кислоты в кислой среде.
Уравнение скорости реакции имеет вид:
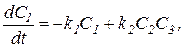
где 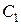 - концентрация хлора,
- концентрация хлора, 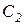 - концентрация хлорноватистой кислоты,
- концентрация хлорноватистой кислоты, 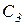 - концентрация соляной кислоты,
- концентрация соляной кислоты, 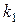 - константа скорости прямой реакции,
- константа скорости прямой реакции, 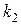 - константа скорости обратной реакции.
- константа скорости обратной реакции.
Так как в любой момент времени хлорноватистая и соляная кислоты образуются в равных концентрациях, то уравнение можно записать в виде :
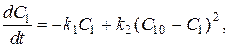
где 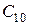 - начальная концентрация хлора.
- начальная концентрация хлора.
В положении равновесия, когда производная равна нулю, выполняется соотношение:
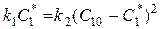 .
.
Сдвинуть равновесие вправо в направлении образования HOCl можно, выводя из реакции любое из веществ в правой части уравнения. Большинство действующих в промышленности производств получают хлорноватистую кислоту нужной концентрации, связывая соляную кислоту. Добиться этого проще всего прибавлением к реакционной смеси какой-нибудь щелочи. Применяя, например, NaOH, имеем:
HCl + NaOH = NaCl + H2O.
Процесс получения хлорноватистой кислоты описывается системой четырех нелинейных дифференциальных уравнений первого порядка:
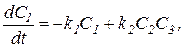
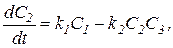
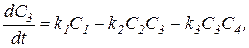
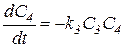 .
.
В этих обозначениях 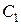 - концентрация хлора,
- концентрация хлора, 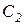 - концентрация хлорноватистой кислоты,
- концентрация хлорноватистой кислоты, 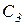 - концентрация соляной кислоты,
- концентрация соляной кислоты,  - концентрация щелочи,
- концентрация щелочи, 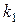 и
и 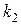 - константы скоростей прямой и обратной реакций в формуле (1),
- константы скоростей прямой и обратной реакций в формуле (1), 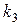 - константа скорости реакции .
- константа скорости реакции .
Константы скоростей отличаются друг от друга на несколько порядков:
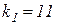 ,
,  ,
, 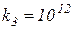 .
.
Как видно из значений констант скоростей система имеет несколько масштабов времени. Для изучения таких разномасштабных систем широко применяется метод квазистационарных концентраций, который предполагает разделение переменных на два класса: быстрые и медленные и позволяет понизить порядок системы.
Используя принцип выявления противоречия, можно считать, что быстрые и медленные реакции – это и есть противоположности, которые умещаются в одной системе.
Разделим третье и четвертое уравнения системы на больший параметр 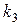 и введем обозначения:
и введем обозначения: 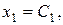
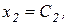
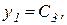
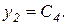
В результате получим систему уравнений с малым параметром при производных:
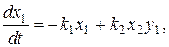
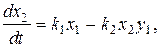
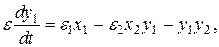
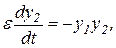
где 
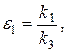
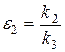 .
.
Таким образом, система разбилась на две подсистемы. Первые два уравнения системы описывают изменение медленных переменных 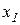 и
и 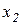 , а вторые два уравнения описывают изменение быстрых переменных
, а вторые два уравнения описывают изменение быстрых переменных 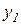 и
и 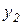 .
.
Дата добавления: 2014-12-12; просмотров: 1030;
