Применение цепей Маркова для анализа социальных систем.
Структура российского общества, как и, очевидно, любого другого, представляет из себя амбивалентную систему, в которой одновременно существуют противоположные классы, например, бедные и богатые, а также их смесь – средний класс. Как указывалась выше, методы теории регулярных Марковских цепей могут быть применены к анализу данных систем.
В качестве основного примера рассмотрим матрицу, показывающую вероятности переходов между тремя слоями населения той или иной страны (данные взяты из исследований, проведенными Глассом и Холлом по Англии и Уэльсу в 1949г.) Получается такая матрица:
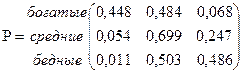
Согласно этой матрице видно, что 44,8% богатых остаются в этом же классе, 48,4% переходят в средний класс и лишь 6,8% разоряются и становятся бедными. Из среднего класса богатыми становятся только 5,4%, 24,7% тоже разоряются и становятся бедными, остальные 69,9% остаются в среднем классе. Лишь 1,1% из бедных становятся богатыми, 50,3% переходят в средний класс и 48,6% остаются бедными.
Согласно неофициальным данным (из газетных публикаций) доля различных слоев населения в России в настоящее время составляет: 5% населения принадлежит к богатым, 75% считаются бедными и остальные 20% - средний класс. Вычислим, как изменится структура общества через определенный интервал времени (шаг цепи Маркова). Умножим вектор строку 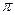 на матрицу переходов P
на матрицу переходов P
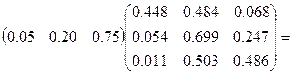
Таким образом, расчет показывает, что для такой матрицы переходов происходит выравнивание структуры общества: количество бедных уменьшилось, численность среднего класса увеличилась, а количество богатых незначительно упало.
Так как цепь регулярная, то представляет интерес найти неподвижный вектор 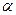 для такой матрицы. Решая соответствующее уравнение для нахождения неподвижного вектора находим, что для нашего примера он равен (0,067; 0,624; 0,309 ), как видно из этого расчета структура российского общества в настоящее время далека от равновесия.
для такой матрицы. Решая соответствующее уравнение для нахождения неподвижного вектора находим, что для нашего примера он равен (0,067; 0,624; 0,309 ), как видно из этого расчета структура российского общества в настоящее время далека от равновесия.
Определим количество шагов, за которое амбивалентная система попадает в установившийся (стационарный) режим, не зависящий от начального распределения вероятностей. Для этого нужно найти ту степень матрицы P, детерминант которой с заданной точностью будет равен детерминанту предельной матрицы A (в идеальном варианте будет равен нулю).
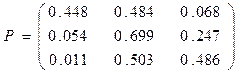
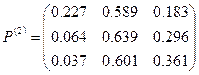
 det
det 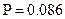
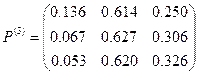
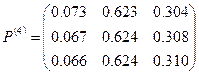
det 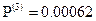
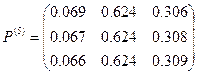
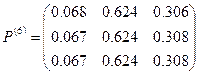
Как видно из приведенных расчетов при количестве шагов равном трем, получаем матрицу, детерминант которой равен 0,00062. По приведенной в теоретическом разделе формуле для количества шагов находим, что при детерминанте исходной матрицы равном 0,086 и точности 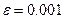 количество шагов равно 2,8 и больше. Также находим фундаментальную матрицу Z, матрицу средних времен достижения M и матрицу для среднеквадратических отклонений времен первого достижения
количество шагов равно 2,8 и больше. Также находим фундаментальную матрицу Z, матрицу средних времен достижения M и матрицу для среднеквадратических отклонений времен первого достижения 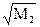 :
:
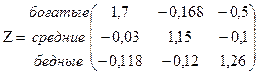 ,
,
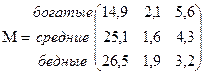 ,
,
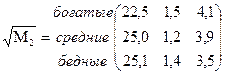 .
.
Из матрицы M для средних времен первого достижения видно, что среднее время перехода из низшего класса в класс богатых почти в пять раз больше, чем время разорения богатых. Настораживает тот факт, что среднеквадратическое отклонение примерно равно среднему времени достижения, т.е. имеет место большой разброс исходных данных.
Согласно теории социальной мобильности, которая характеризует процесс перемещения людей и социальных групп в рамках социальной структуры представляет интерес матрица обмена D 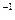 P, которая для нашего примера равна
P, которая для нашего примера равна
D 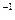 P =
P = 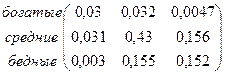 .
.
Матрица обмена показывает что, если амбивалентная система находится в стационарном режиме, то, за определенный интервал времени (шаг цепи), обмен людьми между классами происходит примерно поровну: из богатых в средний класс обмен равен 0,032 и, наоборот, из среднего класса в богатый – 0,031; из богатых в бедняки обмен равен 0,0047 и, наоборот, из бедняков в богатые – 0,003; из среднего класса в бедняки обмен равен 0,156 и, наоборот – 0,155.
Дата добавления: 2014-12-12; просмотров: 1208;
