ТРАНСПОРТНЫЕ СВОЙСТВА ИОНОВ В НЕВОДНЫХ РАСТВОРАХ
Предельная молярная электропроводимость электролита CA определяется предельными подвижностями ионов:
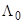 =
= 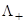 +
+ 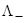
Как известно из общего курса физической химии, подвижность иона связана со скоростью его движения в жидкой среде, 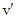 , при бесконечном разведении:
, при бесконечном разведении:
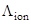 =
= 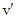 lF/E,
lF/E,
где l – расстояние между электродами, E – разность потенциалов. Поэтому очевидно, что подвижность иона, как и скорость его движения в электрическом поле, должна зависеть от вязкости среды.
В начале XX столетия Писаржевский, а вскоре после него и Вальден заметили, что произведение предельной молярной подвижности данного электролита на вязкость растворителя часто оказывается практически постоянной величиной («числа Писаржевского–Вальдена»). Правда, связь 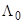 либо подвижности отдельных ионов с вязкостью растворителя отмечалась и в более ранних работах.[15] Вальден считал эту тенденцию весьма общей и называл её правилом. Согласно правилу Вальдена, для данного электролита в различных растворителях должно сохранятся постоянство произведения предельной молярной электропроводимости на вязкость
либо подвижности отдельных ионов с вязкостью растворителя отмечалась и в более ранних работах.[15] Вальден считал эту тенденцию весьма общей и называл её правилом. Согласно правилу Вальдена, для данного электролита в различных растворителях должно сохранятся постоянство произведения предельной молярной электропроводимости на вязкость
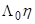 = const
= const
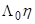
Эта зависимость оказывается удобным подспорьем для прогнозирования значений 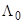 данного электролита в тех растворителях, где они не были определены экспериментально или не могут быть определены из-за невозможности приблизиться сколько-нибудь близко к бесконечному разведению. Последнее обстоятельство имеет место в средах с низкими значениями
данного электролита в тех растворителях, где они не были определены экспериментально или не могут быть определены из-за невозможности приблизиться сколько-нибудь близко к бесконечному разведению. Последнее обстоятельство имеет место в средах с низкими значениями 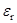 .
.
Пример удовлетворительного выполнения правила Вальдена представлен в таблице 12.
Т а б л и ц а 12
Проверка правила Вальдена для пикрата тетра-н-бутиламмония при 25 оС
| Растворитель | 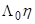 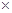 107, Кл2 м–1 моль–1 107, Кл2 м–1 моль–1
|
| Формамид | 53.8 |
| N,N-Диметилформамид | 50.7 |
| Ацетон | 46.2 |
| Ацетонитрил | 47.5 |
| Метанол | 46.7 |
| Этанол | 48.6 |
| Нитробензол | 51.3 |
| Пропиленкарбонат | 55.4 |
Теоретическое обоснование этого эмпирического правила можно получить, сопоставив два выражения для коэффициента диффузии сферического иона радиуса 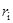 с зарядом
с зарядом 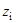 , D, а именно, уравнение Эйнштейна–Смолуховского:
, D, а именно, уравнение Эйнштейна–Смолуховского:
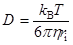
и уравнение Нернста для движения того же иона в электрическом поле:
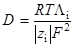 .
.
Приравнивая правые части этих уравнений, получаем соотношение:
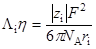
Если при переходе от одного растворителя к другому гидродинамический радиус иона можно считать неизменным, то произведение, стоящее в левой части, действительно должно оставаться постоянным.
Однако наряду с многочисленными подтверждениями правила Вальдена часто наблюдались и отступления от него. В зависимости от природы иона и характера растворителя значение 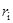 может в той или иной мере изменяться вследствие сольватации, и тогда произведение
может в той или иной мере изменяться вследствие сольватации, и тогда произведение 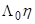 может уже не быть постоянным. Катионы щелочных металлов в некоторых растворителях могут обрастать сольватной «шубой», увеличиваясь в размере. Известны случаи сильного варьирования произведения Писаржевского–Вальдена даже для таких «плохо сольватированных» ионов, как тетрабутиламмоний или тетрафенилборат. Кроме того, для иона водорода H+ высокая подвижность в воде и в спиртах обусловлена хорошо известным «эстафетным» механизмом, что уже не может наблюдаться в негидроксилсодержащих (НДВС) растворителях.
может уже не быть постоянным. Катионы щелочных металлов в некоторых растворителях могут обрастать сольватной «шубой», увеличиваясь в размере. Известны случаи сильного варьирования произведения Писаржевского–Вальдена даже для таких «плохо сольватированных» ионов, как тетрабутиламмоний или тетрафенилборат. Кроме того, для иона водорода H+ высокая подвижность в воде и в спиртах обусловлена хорошо известным «эстафетным» механизмом, что уже не может наблюдаться в негидроксилсодержащих (НДВС) растворителях.
Далее, справедливость правила Вальдена проверялась для растворов с достаточно высокими значениями 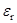 , а для малополярных сред, где
, а для малополярных сред, где 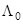 экспериментально найти трудно, уже постулировалась. Но в конце 1950-х годов когда усовершенствовались методы обработки кондуктометрических данных, стало очевидным, что произведение
экспериментально найти трудно, уже постулировалась. Но в конце 1950-х годов когда усовершенствовались методы обработки кондуктометрических данных, стало очевидным, что произведение 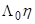 падает с уменьшением диэлектрической проницаемости растворителя. Это отражает, в частности, уравнение Шкодина–Меженного:
падает с уменьшением диэлектрической проницаемости растворителя. Это отражает, в частности, уравнение Шкодина–Меженного:
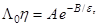
другой подход был предложен несколько ранее Фуоссом
см также Амис
В конце – о связи подвижности ионов с размером и наши данные для ТАА+
Дата добавления: 2014-12-09; просмотров: 2139;
