Дәріс. Кермелеу кезіңде дайындама пішінің және өлшемдерін анықтау

Кермелеу кезіңде дайындама өлшемдерін анықтау қысыммен өңдеу негізгі заңынан шығады: материалдың дайындаманың кермелеуге дейін салмағы (G) және көлемі (V) – дайын бұйымның кермелеуден кейінгі салмаққа (G′) және көлемге (V′) тең болуы керек. Кермелеу кезіңде дайындаманың пішінің және өлшемдерін дұрыс таңдауы материалды пайдалану коэффициентінің максималды жоғарлауына және қалыптаудың технологиялық үрдісін тиімді құрастыруға мүмкіндік береді.

Жазық дайындаманың өлшемдерін анықтау үшін іші қуыс денелерді кермелеудің бес әдісі бар.

Аналитикалық әдістер: беттердің теңдік әдісі, көлемдердің теңдік әдісі, тараздар теңдік әдісі.

Графикалық әдістер: графо-аналитикалық әдіс, графикалық әдіс.

Осы әдістердің әрбірін қысқаша қарастырамыз.

Аналитикалық әдістер. Беттердің теңдік әдісі. Бұл әдіспен материалды жіңішкерусіз кермелеудің қалыпты үрдісі кезіңде пайдалануға болады, т.с.с. s' = s және F' = F болса (қабырғаның орташа қалыңдығы s' дайындама қалыңдығына s тең деп ескерсек). Дайындама ауданы F дайындама дөңгелекшенің ауданы ретіңде болады. Жұқақаңылтырлы материал жағдайы үшін (s 1,5 мм-ге дейін) бұйым ауданы сыртқы диаметр және ішкі биіктігі бойынша, немесе сыртқы диаметрі және ішкі биіктігі бойынша есептелген(түп ауданын қоса отырып), ішкі цилиндр беті түріңде сипатталады. Салыстырмалы қалың материалда цилиндр бетін сыртқы диаметр емес, орташа диаметр арқылы есептейміз. Дайындаманы беттердің теңдік әдісі бойынша есептеуі қаңылтырлы қалыптауда кеңінен тараған.

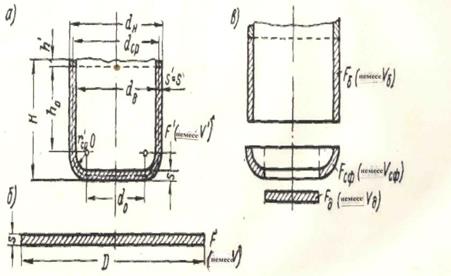
Жәй пішінді іші қуыс айналу денелерінің кермелеуі кезіңде дайындамалардың диаметрін анықтау. Түбі және қабырғаларының қалыңдығы бірдей және шартты тік бұрыш арқылы жанасқан іші қуыс цилиндрді кермелеу кезіңде дайындама өлшемдерін анықтау әдісін қарастырамыз. Қарастырылып отырған бұйымды екі жәй елементтерден тұрады деп есептейміз: цилиндр түбімен және цилиндр түпсіз (40-сурет). 40-суреттен көрініп тұр

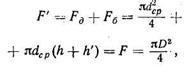(110)

осыдан

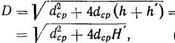(111)

мұндағы h — цилиндрдің ішкі биіктігі; h' — цилиндр қабырғасының шетін қиюға кететін әдіп.

Егер дене n жәй беттерден тұрса, онда әдісті қолдана отырып тәуелділіктен дайындама диаметрін анықтауға болады

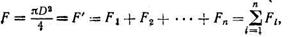(112)

осыдан

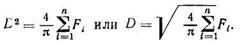(113)

Цилиндр жиегін h' жіңішкеруімен кермелеу кезіңде кесуге кететін әдіп мөлшері материал түріне және қалыңдығына, бұйым пішіні және биіктігіне байланысты әртүрлі болады, сонымен қатар салыстырмалы биіктігіне байланысты өзгереді k_ц =h/d.

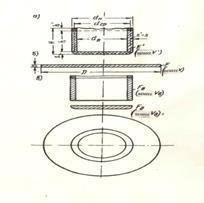
а – бұйым; б – дайындама;в – бұйымның элементтері

40 –сурет. Дайындама өлшемдерін есептеу кезіңде цилиндрлі бұйымның

элементтерге бөлу сүлбесі

0,5 тен 4,0 дейін өзгеретін арақатынас h/d үшін әдіп h'-ті келесі тәуелдіктен анықтаймыз

h мм-мен h' мм-мен

10—50 1—4

50—100 2—6

100—200 3—10

200—300 5—12

Кез-келген күрделі пішінді іші қуыс айналу денелерін кермелеу кезіңде дайындама диаметрін анықтау.

Осы жағдайы үшін дайындама өлшемін белгілі занын қолданып анықтау керек. Бұл заң бойынша кез-келген пішінді АВ = L қисықпен пайда болған (сурет 41) айналу дененің беті F,' өзінің өс уу бойымен қозғалғанда ауырлық ортасы s жасанды қисық 2πх аяққы ұзындығына L шеңбер ұзындығын көбейтуымен анықталады, т.с.с.

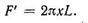(114)

Түп және қабырғаларының бүйірлі беттері сфералық беті бойынша түйінделген цилиндрлі дайындаманың өлшемін анықтау жағдайын қарастырамыз (32-сурет). Бұл дене үш элементтерден тұрады деп қарастырамыз: (түпсіз) цилиндр, жұмырланған бөлімдердің бұйым және түп өс айналасыңда айналуымен пайда болған беттер.

Беттердің теңдік шарттарынан сурет 42-де келтірілген геометриялық арақатынастарды және белгіленулерді қолдана отырып, мынаны жазуға болады

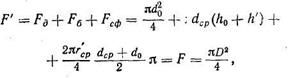(115)

осыдан

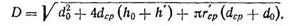(116)

Сфералық беттер үшін F_сф теңдуі жуықталған, ал тәжірибеге мақсатында толық жарайды.

Көлемдер теңдік әдісі. Бұл әдіспен бүйірлі қабырғаларының қалыңдығы бастапқы дайынданың және түп қалыңдығының айырмашылығы бар болған кезде, егер s' ≠ s және F' ≠ F материалды жіңішкеруімен кермелеу кезіңде қолдануы дұрыс.

а-бұйым; б – дайындама; в – бұйымның элементтері

42 –сурет Дайындама өлшемдерін есептеу үшін цилиндрлік бұйымды түбін жұмырлауымен элементтерге бөлу сүлбесі

Іші қуыс цилиндрді кермелеу кезіңде, оның бүйірлі қабырғалары және түбі әртүрлі қалыңдықты және шартты түрде тік бұрышпен түіндеседі (сурет 30, егер s' <s болса), осы көлемнің теңдік шартынан V′ = V, тең деп аламыз

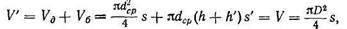(117)

осыдан

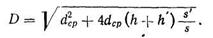(118)

Цилиндрдің бүйірлі қабырғалары және түбі әртүрлі қалыңдықты және сфералық беттеріңде жанасқан кезде, дайындама өлмдері ұқсас анықталады. Қабырғаларын жіңішкеруімен іші қуыс созылған цилиндрлерді кесу кезіңде қалдықтардың мөлшері материал түрінен және қалыңдығынан, салыстырмалы биіктік h/d және операциялар санына байланысты болады. Жуықтап арақатынасы h/d 2 ден 10 дейін өзгерсе, қалдық тетік көлемінің 8 ден 12% дейін құрайды, ал ұлкен арақатынастарда - 12 ден 15% құрайды.Кез-келген жәй көлем санымен пайда болған, іші қуыс айналу денелерін кермелеу үшін дайындама өлшемдерін мына теңдеуден анықтаймыз

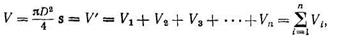(119)

осыдан

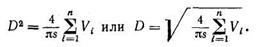(120)

Тараздар теңдік әдісі. Бұйымның дайын үлгісі болған кезде, тараздар теңдік әдісі арқылы дайындама диаметрін анықтау оңай болады.

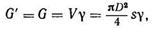(121)

осыдан

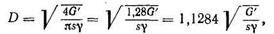(122)

мұндағы D — дайындама диаметрі см-мен; s — дайындама қалыңдығы см-мен;G' — бұйым салмағы г-мен; γ — меншікті салмағы г/см³-мен.

Тәжірибе жүзіңде күрделі айналу іші қуыс денелер үшін бұл әдістер қолданылмайды, өйткені күрделі теңдеулерді шешуі өте қиынға соғады және көп уақыт шығынын талап етеді. Ұқсас жағдайларда дайындамалардың өлшемдерін анықтау үшін графо-аналитикалық немесе графикалық әдістерді пайдалануды қолайлы болады.

Графо-аналитиқалық әдіс. Бұл әдістің маңыздылығы х арақашықтығымен ауырлық ортасынан кез-келген кесіндіні айналу өсіне дейін, оның ұзындығын L-ды, т.с.с. аналитикалық мөлшерін анықтау белгілі қиындықтармен жанасқан. Негізінен осы жағдайда графикалық түрде шешуі, кейбір графикалық қосындысымен, сол сияқты аталған мөлшерлерді интегралдаумен сонымен қатар графикалық жолмен анықтауы аяғында дайындама диаметрін аналитикалық жолмен шешуіне кетеді.

уу өс айналасында айналған АВ қисық жасаушымен пайда болған (сурет 33) іші қуыс айналу денелі тетік алсақ, онда қисық АВ-ны айналу өсі уу ауырлық ортасынан s₁, s₂…, s_n сәйкес арақашықтықты r₁, r₂, ..., r_п тік кесінді ретіңде үлкен қателіктіз қарастырып кішкентай бөліктерге l₁, l₂, ..., l_n осылай бөлу керек. Арақашықтық r₁, r₂, ..., r_п айналу элемент қисықтар радиустарын айналу дене беттерін элементарлы беттер қосындысы ретіңде алуымыз тиіс, т.с.с.

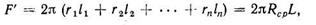(123)

мұндағы (124)

Егер

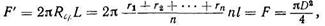(125)

осыдан

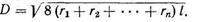(126)

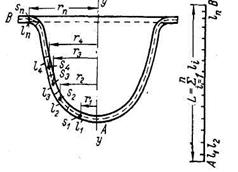
43 –сурет. Дайындама өлшемдерін графо-аналитикалық әдіспен есептеу кезіңде күрделі айналу денелердің элементтерге бөлу сүлбесі

Мұнда R_cp= 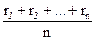^- жасаушы қисықтың айналу ауыр ортасының радиусы.

Графикалық әдіс. Жасаушы қисық ауырлық ортасынан айналу өсіне дейін арақашықтығын графикалық түрмен анықтау жіпті көпбұрыш арқылы іске асады (34-сурет). Бұл әдіс негізіңде үлкейтілген масштабыңдағы жасаушы қисық АВ бұйым қарамын жасаушы бөліктерге бөледі. Бөлек бөліктердің ауырлық ортасы (s₁,s₂, .... s_n) айналу өсі уу арқылы тік сызықтар жүргізіледі (44-сурет, а). Содан кейін бөлек бөліктердің ауырлық күшінің теңәсерлі орнын анықтау үшін жіпті көпбұрыштық құрылады.

Ұзындықтырына пропорционалды бөлек бөліктердің жасаушы кесінділері L₁, L₂, ..., L_n бір сызық АС-та бірізділі бірінін артынан бірі көрініп шыға бастайды және кез-келген таңдалып алынған О нүктесінен осы кесінділердің аяғына сәулелер (1,2, ..., n, n+1) жүргізіледі. Содан кейін негізгі сызбада (сурет 44, б) осы сәулелерге параллельді сызықтар жүргізеді (сәуле 1′, 2' және т. б.).

Шеткі сызықтар (сәуле) 1' және (n + 1)' дейін бірімен-бірі қиылысқанша тоқтамайды; айналу өсінен уу шеткі сәулелер киылысқан нүктесі арқылы жүргізілген NN сызығына дейін арақашықтық және айналу өсі жасаушы қисық АВ-дан ауырлық ортасына дейін R_s арақашықтығы ретіңде көрсетіліп тұр. Жасаушы ұзындығы сызбадан белгіленеді. Ал ары қарай белгілі беттер теоремасы негізіңде құралады

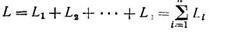(127)

Айналу денелеріне мына теңдеуді қолданамыз.

осыдан

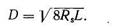(128)

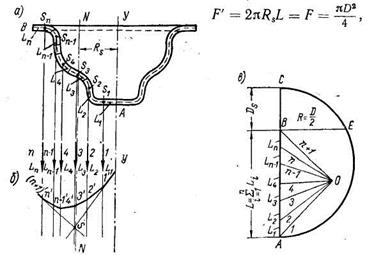
а — бұйым; б — жіпті көпбұрышты құрастыру сүлбесі; в — дайындама диаметрін графикалық түрде анықтау

44 –сурет. Дайындама өлшемдерін графикалық әдіспен анықтау сүлбесі

Дайындама диаметрін графикалық түрде анықтайық. (121) теңдеуді мына түрге келтіруге болады

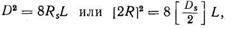(129)

осыдан

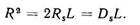(130)

Тікбұрыш ұшынан гипотенузаға түсірген перпендикуляр, гипотенуза кесінділер арасыңда орташа пропорционалды деп белгілі теореманы қолданамыз. Тік сызық АВ-ны жалғастыра отырып (сурет 44, в) диаметрде D мөлшерін өлшеп орнатып, содан кейін жартышеңберді сызып және В нүктесіңде BE перпендикулярын АС тік сызығына дейін жеткізіп орнатамыз. BE кесіндісі радиусы R = D/2 тең дайындама түріңде анықталады.

Ұсынылған әдебиет: Нег. 1[195-207] қос. 2[117-146]