Движение частиц при наличии потенциального барьера бесконечной ширины.

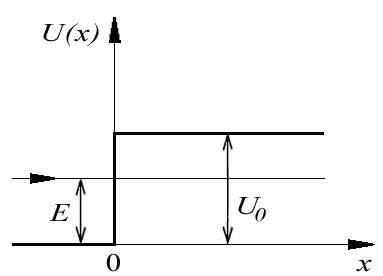
Рассмотрим движение частицы поле, потенциальная энергия U(x) которого имеет вид:

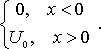
Уравнение Шредингера для области I имеет вид: 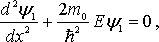а для области II:

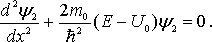
Рассмотрим сначала случай, когда энергия E частицы меньше высоты потенциального барьера Uo , т.е. E<Uo. Говорят, что в этом случае мы имеем дело с высоким потенциальным барьером. Введем:

I zUvOT8nMS7dVCg1x07VQUiguScxLSczJz0u1VapMLVayt+PlAgAAAP//AwBQSwMEFAAGAAgAAAAh AH1u26TBAAAA3AAAAA8AAABkcnMvZG93bnJldi54bWxET0tqwzAQ3QdyBzGB7mI5gbbGjRJKQqCF bvI5wMSaWG6lkZGU2L19VSh0N4/3ndVmdFbcKcTOs4JFUYIgbrzuuFVwPu3nFYiYkDVaz6TgmyJs 1tPJCmvtBz7Q/ZhakUM41qjApNTXUsbGkMNY+J44c1cfHKYMQyt1wCGHOyuXZfkkHXacGwz2tDXU fB1vTsFlKJ/Du99/3q4XGz929lAZHpV6mI2vLyASjelf/Od+03l+9Qi/z+QL5PoHAAD//wMAUEsB Ai0AFAAGAAgAAAAhAASrOV4AAQAA5gEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVz XS54bWxQSwECLQAUAAYACAAAACEACMMYpNQAAACTAQAACwAAAAAAAAAAAAAAAAAxAQAAX3JlbHMv LnJlbHNQSwECLQAUAAYACAAAACEAMy8FnkEAAAA5AAAAEgAAAAAAAAAAAAAAAAAuAgAAZHJzL3Bp Y3R1cmV4bWwueG1sUEsBAi0AFAAGAAgAAAAhAH1u26TBAAAA3AAAAA8AAAAAAAAAAAAAAAAAnwIA AGRycy9kb3ducmV2LnhtbFBLBQYAAAAABAAEAPcAAACNAwAAAAA= " fillcolor="#cc9" strokecolor="#036"> 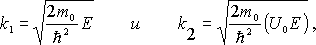Получаем следующие уравнения Шредингера для областей I и II:

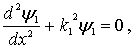
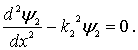Решения этих уравнений имеют следующий вид:

I zUvOT8nMS7dVCg1x07VQUiguScxLSczJz0u1VapMLVayt+PlAgAAAP//AwBQSwMEFAAGAAgAAAAh AEv+etXCAAAA3AAAAA8AAABkcnMvZG93bnJldi54bWxET01rAjEQvQv9D2GE3jSriJXV7NIKlkoP pdtevI2bMbt0M1mSVNd/3whCb/N4n7MpB9uJM/nQOlYwm2YgiGunWzYKvr92kxWIEJE1do5JwZUC lMXDaIO5dhf+pHMVjUghHHJU0MTY51KGuiGLYep64sSdnLcYE/RGao+XFG47Oc+ypbTYcmposKdt Q/VP9WsV+Cf5/iJp0b0ePva8wKMxS2eUehwPz2sQkYb4L76733Sav5rD7Zl0gSz+AAAA//8DAFBL AQItABQABgAIAAAAIQAEqzleAAEAAOYBAAATAAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9UeXBl c10ueG1sUEsBAi0AFAAGAAgAAAAhAAjDGKTUAAAAkwEAAAsAAAAAAAAAAAAAAAAAMQEAAF9yZWxz Ly5yZWxzUEsBAi0AFAAGAAgAAAAhADMvBZ5BAAAAOQAAABIAAAAAAAAAAAAAAAAALgIAAGRycy9w aWN0dXJleG1sLnhtbFBLAQItABQABgAIAAAAIQBL/nrVwgAAANwAAAAPAAAAAAAAAAAAAAAAAJ8C AABkcnMvZG93bnJldi54bWxQSwUGAAAAAAQABAD3AAAAjgMAAAAA " fillcolor="#cc9" strokecolor="#036">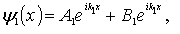

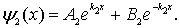
Волновая функция на границе раздела областей I и II должна быть не только непрерывной, но и гладкой, т.е. иметь непрерывную производную. Приравнивание волновых функций и их производных на границе раздела двух областей, в которых волновая функция имеет разный вид, получило название сшивки волновых функций и их производных. В данном случае условия сшивки имеют вид:

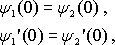что приводит к: 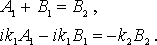Положим А1=1, а А2=0, т.к. нет условий для отражения в области II. Остальные коэффициенты имеют следующий вид:

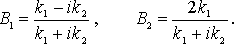Тогда волновые функции можно записать в следующем виде:

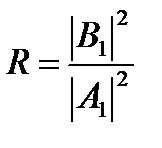
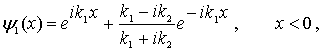
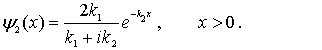Найдем коэффициент отражения, определяющий вероятность того, что частица отразится от высокого порога. Согласно физическому смыслу, коэффициент отражения R

После подстановки полуим:

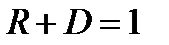
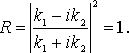Коэффициент прохождения D частицы через барьер определяется из условия:

Т.е D=0. Плотность вер-ти нахождения частицы в обл 2:

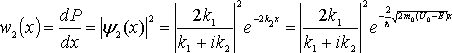Т.е. при малых x вероятность обнаружить частицу в области II отлична от нуля: