Частица в потенциальной яме конечной глубины
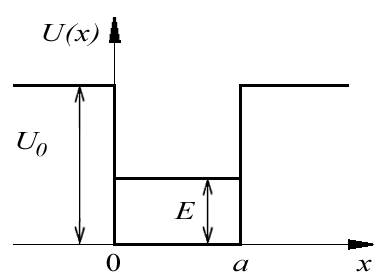
Рассмотрим частицу, находящуюся в области потенциальной прямоугольной ямы конечной глубины (рис.4.20) . Такая модель качественно описывает
|
| Рис. 4.21. |
движение заряженной частицы, например электрона, вблизи атома и применяется в атомной физике и физике твердого тела. Пусть потенциальная энергия частицы имеет вид
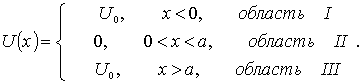
Рассмотрим сначала случай 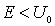 , т.е. будем считать, что частица находится в яме. Уравнение Шредингера в областях I и III ( вне потенциальной ямы) записывается в виде
, т.е. будем считать, что частица находится в яме. Уравнение Шредингера в областях I и III ( вне потенциальной ямы) записывается в виде
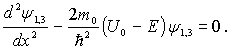
Вводя обозначение 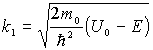 , получаем
, получаем
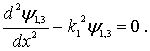
Решения этого уравнения имеют вид
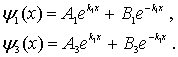
Для того, чтобы волновая функция была ограничена, нужно потребовать, чтобы 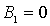 и
и 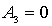 .
.
В области II , т.е. внутри потенциальной ямы, уравнение Шредингера
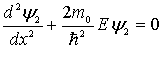
имеет осциллирующее решение 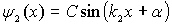 , где
, где 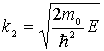 .
.
Таким образом, волновые функция частицы для данной задачи имеют вид
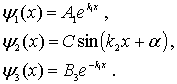
|
Дата добавления: 2014-12-06; просмотров: 2518;
