Частица в потенциальной яме бесконечной глубины

Такая потенциальная «яма» описывается следующими соотношениями для потенциальной энергии (рис.4):

U =  в областях 1, 3 для x < 0 и x > a; U = 0 в области 2 для 0> x >a.

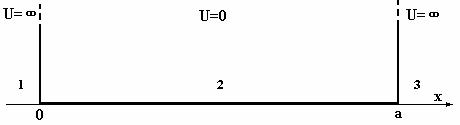
Рис.4. График потенциала одномерной бесконечно глубокой «ямы».

Запишем стационарное уравнение Шредингера для областей 1, 3 , где U=

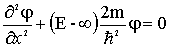, (1.14)

его единственно возможное решение =0. Это означает, что вероятность нахождения частицы в этих областях равна нулю и частица туда проникнуть не может.

Для области 2 стационарное уравнение Шредингера имеет вид

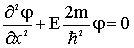, (1.15)

из теории дифференциальных уравнений следует, что его решение имеет вид

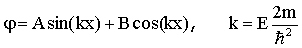. (1.16)

Вследствие требования непрерывности функции , она должна быть равна нулю в точках x=0 и x=a, что следует из решения для областей 1, 3. Отсюда получается, что должны выполняться соотношения Asin(0)+Bcos(0)=0, Asin(ka)+Bcos(ka)=0 и, согласно математике, это будет при B=0 и ka=n, где n-целое число. Необходимое также условие нормировки (1.12) в данной задаче имеет вид

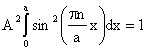, (1.17) sin²x= (1-cos2x)/2

взяв этот интеграл, получаем 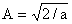и в результате имеем конечное выражение для возможных решений уравнения Шредингера в поставленной задаче

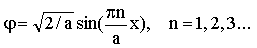. (1.18) (возвести в квадрат)= плотность вероятности

Данное решение показывает, что поведение микрочастицы в одномерной бесконечно глубокой потенциальной «яме» может быть различным в зависимости от значения числа n, его называют квантовым числом и рассматривают как номер возможного состояния микрочастицы.