Прохождение частицы через потенциальный барьер конечной длины

U(x)=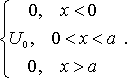

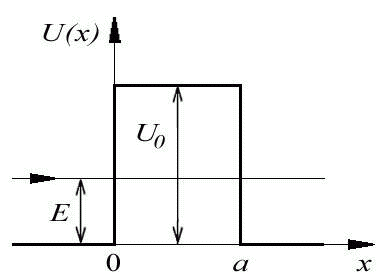
Уравнение Шредингера для каждой из областей:

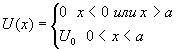
Поскольку при заданных условиях потенциальная энергия U не может быть записана в виде аналитической функции, мы напишем уравнение Шредингера отдельно для областей (I), (III) (где потенциальные энергии одинаковы, U₀ = 0) и для области (II) и найдем решения в обоих случаях, т.е. функции Ψ_{1, 3} и Ψ₂. На границе при x = 0 в силу непрерывности волновой функции и ее производной приравняем Ψ₁ и Ψ₂ и их первые производные. Проделаем то же при x = a для функций Ψ₂ и Ψ₃. Это позволит найти необходимые коэффициенты.

Итак, пишем уравнения Шредингера:

для областей (I, III)

,

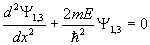для области (II)

,

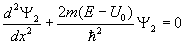где m и E – масса и полная энергия частицы, соответственно. Введем обозначения

.

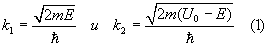Уравнения приобретают вид

.

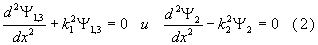Общие решения уравнений (1) таковы:

.

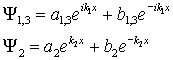В областях (I, III) это бегущие плоские волны, а в области (II)- затухающая волна.

Отличие рассматриваемой задачи от изученных в лекции "Рассеяние частиц. Одномерное движение" состоит в том, что здесь отражение имеет место как на границе областей (I) и (II), так на границе (II) и (III). Поскольку в области (III) потенциал постоянен, отражения нет, и коэффициент b₃ = 0.

Для нас представляет интерес в первую очередь коэффициент прохождения D, который есть отношение

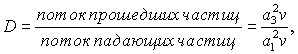
где v - скорость частицы. Она одинакова для всех частиц в областях I и III.

Применяя граничные условий к волновым функциям позволяет получить следующее выражение для коэффициента прохождения: 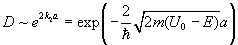.Эта формула показывает, во-первых, что коэффициент прохождения не равен нулю, во-вторых, его величина очень сильно зависит от ширины барьера a.