Теорема Маркова о шифрах, не распространяющих искажение

Нормальный алгоритм (алгорифм) Маркова (НАМ, также Марковский алгоритм) — один из стандартных способов формального определения понятия алгоритма (другой известный способ — машина Тьюринга). Понятие нормального алгоритма введено А. А. Марковым (младшим) в конце 1940-х годов в работах по неразрешимости некоторых проблем теории ассоциативных вычислений. Традиционное написание и произношение слова «алгорифм» в этом термине также восходит к его автору, многие годы читавшему курс математической логики на механико-математическом факультете МГУ.

Нормальный алгоритм описывает метод переписывания строк, похожий по способу задания на формальные грамматики. НАМ является Тьюринг-полным языком, что делает его по выразительной силе эквивалентным машине Тьюринга и, следовательно, современным языкам программирования. На основе НАМ был создан функциональный язык программирования Рефал.

Нормальные алгоритмы являются вербальными, то есть предназначенными для применения к словам в различных алфавитах.

Определение всякого нормального алгоритма состоит из двух частей: определения алфавита алгоритма (к словам из символов которого алгорифм будет применяться) и определения его схемы. Схемой нормального алгоритма называется конечный упорядоченный набор так называемых формул подстановки, каждая из которых может быть простой или заключительной. 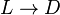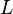Простыми формулами подстановки называются слова вида ,где и 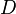— два произвольных слова в алфавите алгоритма (называемые, соответственно, левой и правой частями формулы подстановки). 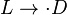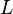Аналогично, заключительными формулами подстановки называются слова вида ,где и 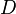— два произвольных слова в алфавите алгоритма. При этом предполагается, что вспомогательные буквы \to и \to\cdot не принадлежат алфавиту алгоритма (в противном случае на исполняемую ими роль разделителя левой и правой частей следует избрать другие две буквы).

Примером схемы нормального алгоритма в пятибуквенном алфавите |*abc может служить схема

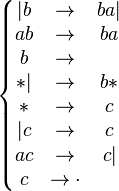
Процесс применения нормального алгоритма к произвольному слову V в алфавите этого алгоритма представляет собой дискретную последовательность элементарных шагов, состоящих в следующем. Пусть V' — слово, полученное на предыдущем шаге работы алгорифма (или исходное слово V, если текущий шаг является первым). Если среди формул подстановки нет такой, левая часть которой входила бы в V', то работа алгорифма считается завершённой, и результатом этой работы считается слово V'. Иначе среди формул подстановки, левая часть которых входит в V', выбирается самая первая. Если эта формула подстановки имеет вид 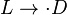,, то из всех возможных представлений слова V' в виде RLS выбирается такое, при котором R — самое короткое, после чего работа алгорифма считается завершённой с результатом RDS. Если же эта формула подстановки имеет вид 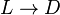, то из всех возможных представлений слова V' в виде RLS выбирается такое, при котором R — самое короткое, после чего слово RDS считается результатом текущего шага, подлежащим дальнейшей переработке на следующем шаге.

Например, в ходе процесса применения алгорифма с указанной выше схемой к слову |*|| последовательно возникают слова |b*|, ba|*|, a|*|, a|b*, aba|*, baa|*, aa|*, aa|c, aac, ac| и c||, после чего алгорифм завершает работу с результатом ||. Другие примеры смотрите ниже.

Любой нормальный алгорифм эквивалентен некоторой машине Тьюринга, и наоборот — любая машина Тьюринга эквивалентна некоторому нормальному алгорифму. Вариант тезиса Чёрча — Тьюринга, сформулированный применительно к нормальным алгорифмам, принято называть «принципом нормализации».

Нормальные алгорифмы оказались удобным средством для построения многих разделов конструктивной математики. Кроме того, заложенные в определении нормального алгорифма идеи используются в ряде ориентированных на обработку символьной информации языков программирования — например, в языке Рефал.

Булева функция (или логическая функцияот n аргументов — в дискретной математике — отображение B_n → B, где B = {0,1} — булево множество. Элементы булева множества {1, 0} обычно интерпретируют как логические значения «истинно» и «ложно», хотя в общем случае они рассматриваются как формальные символы, не несущие определённого смысла. Неотрицательное целое число n называют арностью или местностью функции, в случае n = 0 булева функция превращается в булеву константу. Элементы декартова произведения (n-я прямая степень) B_n называют булевыми векторами. Множество всех булевых функций от любого числа аргументов часто обозначается P₂, а от n аргументов — P₂(n). Переменные, принимающие значения из булева множества называются булевыми переменными. Булевы функции названы по фамилии математика Джорджа Буля.

При работе с булевыми функциями происходит полное абстрагирование от содержательного смысла, который имелся в виду в алгебре высказываний. Тем не менее, между булевыми функциями и формулами алгебры высказываний можно установить взаимно-однозначное соответствие, если:

· установить взаимно-однозначное соответствие между булевыми переменными и пропозициональными переменными,

· установить связь между булевыми функциями и логическими связками,

· оставить расстановку скобок без изменений.

Нормализация — приведение чего-либо в нормальное состояние.

Криптография решает такие проблемы безопасности информации как конфиденциальность, целостность, аутентификация и невозможность отказа сторон от авторства. Первые три уже упоминались ранее. Однако именно с появлением криптографических средств невозможность отказа от авторства (предотвращение отказа абонента от совершенных им действий) стало возможным. Когда речь идет о криптографии, то в первую очередь речь идет о всевозможном шифровании. Шифры – совокупность обратимых преобразований множества открытых данных на множество закрытых данных. Конкретный вид преобразования определяется секретным параметром – ключом шифра. Теперь определимся с терминологией:

· Зашифрование – перевод информации из открытой формы в закрытую форму;

· Расшифрование – перевод информации из закрытой формы в открытую форму (ключ известен);

· Дешифрование – перевод информации из закрытой формы в открытую форму без ключа (взлом);

· Шифрование – зашифрование или расшифрование.

Классификации шифров представлена на рисунке 1.

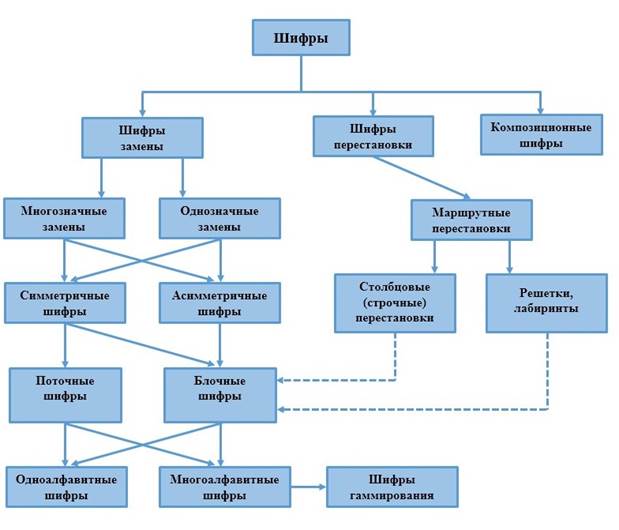
Рис. 1 – Классификация шифров

Тема 5