Основные алгебраические структуры, применяемые в криптографии

Алгебраическая система (или алгебраическая структура) в универсальной алгебре — множество G (носитель) с заданным на нём набором операций и отношений (сигнатура), удовлетворяющим некоторой системе аксиом. Алгебраическая система с пустым множеством отношений называется алгеброй, а система с пустым множеством операций — моделью.

n-арная операция на G — это отображение прямого произведения n экземпляров множества в само множество 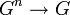. По определению, 0-арная операция — это просто выделенный элемент множества. Чаще всего рассматриваются унарные и бинарные операции, поскольку с ними легче работать. Но в связи с нуждами топологии, алгебры, комбинаторики постепенно накапливается техника работы с операциями большей арности, здесь в качестве примера можно привести теорию операд (клонов полилинейных операций) и алгебр над ними (мультиоператорных алгебр).

Для алгебраических систем естественным образом определяются морфизмы как отображения, сохраняющие операцию. Таким образом определяются категории групп, колец, R-модулей и т. п.

Если множество обладает структурой топологического пространства, и операции являются непрерывными, то его называют топологической алгебраической системой. Так, в топологической группе операции умножения и взятия обратного элемента являются непрерывными.

Не все алгебраические конструкции описываются алгебраическими системами, в качестве примера таковых можно упомянуть коалгебры, биалгебры, алгебры Хопфа и комодули над ними.

Криптографические методы защиты информации - это специальные методы шифрования, кодирования или иного преобразования информации, в результате которого ее содержание становится недоступным без предъявления ключа криптограммы и обратного преобразования. Криптографический метод защиты, безусловно, самый надежный метод защиты, так как охраняется непосредственно сама информация, а не доступ к ней (например, зашифрованный файл нельзя прочесть даже в случае кражи носителя). Данный метод защиты реализуется в виде программ или пакетов программ.

Современная криптография включает в себя четыре крупных раздела:

1. Симметричные криптосистемы.

В симметричных криптосистемах и для шифрования, и для дешифрования используется один и тот же ключ. (Шифрование - преобразовательный процесс: исходный текст, который носит также название открытого текста, заменяется шифрованным текстом, дешифрование - обратный шифрованию процесс. На основе ключа шифрованный текст преобразуется в исходный);

2. Криптосистемы с открытым ключом.

В системах с открытым ключом используются два ключа - открытый и закрытый, которые математически связаны друг с другом. Информация шифруется с помощью открытого ключа, который доступен всем желающим, а расшифровывается с помощью закрытого ключа, известного только получателю сообщения. (Ключ - информация, необходимая для беспрепятственного шифрования и дешифрования текстов.);

3. Электронная подпись.

Системой электронной подписи. называется присоединяемое к тексту его криптографическое преобразование, которое позволяет при получении текста другим пользователем проверить авторство и подлинность сообщения.

4. Управление ключами.

Это процесс системы обработки информации, содержанием которых является составление и распределение ключей между пользователями.

Основные направления использования криптографических методов - передача конфиденциальной информации по каналам связи (например, электронная почта), установление подлинности передаваемых сообщений, хранение информации (документов, баз данных) на носителях в зашифрованном виде.

Требования к криптосистемам

Процесс криптографического закрытия данных может осуществляться как программно, так и аппаратно. Аппаратная реализация отличается существенно большей стоимостью, однако ей присущи и преимущества: высокая производительность, простота, защищенность и т.д. Программная реализация более практична, допускает известную гибкость в использовании.

Для современных криптографических систем защиты информации сформулированы следующие общепринятые требования:

· зашифрованное сообщение должно поддаваться чтению только при наличии ключа;

· число операций, необходимых для определения использованного ключа шифрования по фрагменту шифрованного сообщения и соответствующего ему открытого текста, должно быть не меньше общего числа возможных ключей;

· число операций, необходимых для расшифровывания информации путем перебора всевозможных ключей должно иметь строгую нижнюю оценку и выходить за пределы возможностей современных компьютеров (с учетом возможности использования сетевых вычислений);

· знание алгоритма шифрования не должно влиять на надежность защиты;

· незначительное изменение ключа должно приводить к существенному изменению вида зашифрованного сообщения даже при использовании одного и того же ключа;

· структурные элементы алгоритма шифрования должны быть неизменными;

· дополнительные биты, вводимые в сообщение в процессе шифрования, должен быть полностью и надежно скрыты в шифрованном тексте;

· длина шифрованного текста должна быть равной длине исходного текста;

· не должно быть простых и легко устанавливаемых зависимостью между ключами, последовательно используемыми в процессе шифрования;

· любой ключ из множества возможных должен обеспечивать надежную защиту информации;

· алгоритм должен допускать как программную, так и аппаратную реализацию, при этом изменение длины ключа не должно вести к качественному ухудшению алгоритма шифрования.

Симметричные криптосистемы

Все многообразие существующих криптографических методов в симметричных криптосистемах можно свести к следующим 4 классам преобразований:

· подстановка - символы шифруемого текста заменяются символами того же или другого алфавита в соответствии с заранее определенным правилом;

· перестановка - символы шифруемого текста переставляются по некоторому правилу в пределах заданного блока передаваемого текста;

· аналитическое преобразование - шифруемый текст преобразуется по некоторому аналитическому правилу, например, гаммирование - заключается в наложении на исходный текст некоторой псевдослучайной последовательности, генерируемой на основе ключа;

· комбинированное преобразование - представляют собой последовательность (с возможным повторением и чередованием) основных методов преобразования, применяемую к блоку (части) шифруемого текста. Блочные шифры на практике встречаются чаще, чем “чистые” преобразования того или иного класса в силу их более высокой криптостойкости. Российский и американский стандарты шифрования основаны именно на этом классе.

Системы с открытым ключом

Как бы ни были сложны и надежны криптографические системы - их слабое мест при практической реализации - проблема распределения ключей. Для того, чтобы был возможен обмен конфиденциальной информацией между двумя субъектами ИС, ключ должен быть сгенерирован одним из них, а затем каким-то образом опять же в конфиденциальном порядке передан другому. Т.е. в общем случае для передачи ключа опять же требуется использование какой-то криптосистемы. Для решения этой проблемы на основе результатов, полученных классической и современной алгеброй, были предложены системы с открытым ключом.

Для того, чтобы гарантировать надежную защиту информации, к системам с открытым ключом предъявляются два важных и очевидных требования:

1. Преобразование исходного текста должно быть необратимым и исключать его восстановление на основе открытого ключа.

2. Определение закрытого ключа, на основе открытого также должно быть невозможным на современном технологическом уровне. При этом желательна точная нижняя оценка сложности (количества операций) раскрытия шифра.

Алгоритмы шифрования с открытым ключом получили широкое распространение в современных информационных системах. Так, алгоритм RSA стал мировым стандартом де-факто для открытых систем. Вообще же все предлагаемые сегодня криптосистемы с открытым ключом опираются на один из следующих типов необратимых преобразований:

· Разложение больших чисел на простые множители;

· Вычисление логарифма в конечном поле;

· Вычисление корней алгебраических уравнений.

Электронная подпись

В конце обычного письма или документа исполнитель или ответственное лицо обычно ставит свою подпись. Подобное действие обычно преследует две цели. Во-первых, получатель имеет возможность убедиться в истинности письма, сличив подпись с имеющимся у него образцом. Во-вторых, личная подпись является юридическим гарантом авторства документа. Последний аспект особенно важен при заключении разного рода торговых сделок, составлении доверенностей, обязательств и т.д. Если подделать подпись человека на бумаге весьма непросто, а установить авторство подписи современными криминалистическими методами - техническая деталь, то с подписью электронной дело обстоит иначе. Подделать цепочку битов, просто ее скопировав, или незаметно внести нелегальные исправления в документ сможет любой пользователь. С широким распространением в современном мире электронных форм документов (в том числе и конфиденциальных) и средств их обработки особо актуальной стала проблема установления подлинности и авторства безбумажной документации. В разделе криптографических систем с открытым ключом было показано, что при всех преимуществах современных систем шифрования они не позволяют обеспечить аутентификацию данных. Поэтому средства аутентификации должны использоваться в комплексе и криптографическими алгоритмами.

Тема 4