Основы математической теории информации

Целлюлоза мен крахмалдын айырмашылығы мен ұқсастықтары қандай?

Целлюлозаның қасиеттерін айтып беріңдер.

Өнеркәсіптік маңызы бар химиялық қасиеттерінің теңдеулерін жазыңдар.

Целлюлоза қайда қолданылады?

Көмірсулардың адам тіршілігіндегі маңызы қандай?

Құрамында 20% крахмал бар 10 кг картоптан қанша глюкоза алуға болады?

Егер шығымы 75% болса, 32,4 кг целлюлозадан қанша триацетилцеллюлоза алуға болады?

Тема 1

Основы математической теории информации

Теория информамции

К.Шеннон является основателем Теории информации. В своей работе "Математическая теория связи" К. Шеннон, используя статистический подход к определению количества информации (в котором оценка информации определяется с точки зрения меры неопределенности, снимаемой при получении информации), показал, что количество информации удобно измерять с помощью энтропии.

Энтропия H(X)— мера неопределённости случайной величины X, выражаемая следующей формулой

,

где 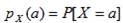обозначает вероятность того, что случайная величина X примет значение a. Это означает, что с вероятностью 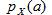X может быть описана битами информации.

Модель Шеннона

Симметричные криптосистемы использовались более двух тысяч лет (вспомните шифр Цезаря), однако формальное математическое описание таких систем было дано Клодом Шенноном только в 1949 году. Подход Шеннона превратил криптографию из искусства в науку, так как появилась возможность доказывать защищенность информации при помощи шифра. Однако реализация последовательности независимых и равновероятных случайных величин оказалась непростой задачей. Кроме того, объем ключа в совершенном шифре совпадает с объемом сообщения, что затрудняет выполнение условия секретности ключа.

По К. Шеннону, шифрование должно использовать следующие принципы:

· Рассеивание (Diffusion) — распространение влияния одного знака открытого текста на более, чем один знак шифртекста, а также распространение влияния одного элемента ключа на более, чем один знак шифртекста.

· Перемешивание, усложнение, запутывание (Confusion) — свойство шифрующего преобразования усложнять взаимосвязи между элементами данных, что затрудняет восстановление функциональных и статистических связей между открытым текстом, ключом и шифртекстом.

Эти два общих принципа конструирования криптосистемы – очень общие и неформальные. Шеннон также описал более специфичные принципы конструирования. Первый заключается в том, чтобы свести проблему обеспечения секретности системы к одной из известных вычислительно сложных задач. Этот принцип часто используется при создании криптосистем с открытым ключом, но не используется для криптосистем с секретным ключом. Второй принцип Шеннона заключается в том, чтобы сделать систему устойчивой ко всем известным атакам, и это до сих пор лучший из известных принципов построения криптосистем с секретным ключом.

В описании криптосистемы, данном Шенноном, отправитель А (часто называемый Алисой) хочет отправить сообщение m получателю В (которого называют Бобом). Сообщение называется открытым текстом и берется из конечного набора открытых текстов М. Конечно, Алиса может отправить более одного сообщения.

Из-за того, что канал связи не защищен (противник, называемый Евой, также

имеет доступ к каналу), Алиса применяет алгоритм шифрования к тексту m. Результат называют шифртекстом, он является элементом набора шифртекстов С. Алиса передает Бобу шифртекст C, который будет перехвачен Евой. Очевидно, что функция шифрования должна быть биективным отображением, иначе Боб не сможет восстановить открытый текст m по шифртексту с с помощью функции расшифрования 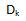. По формуле 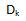(c)=m.

Так как той же самой криптосистемой хотят воспользоваться другие люди, а Алиса и Боб не хотят использовать одно и то же отображение 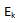в течение долгого времени из соображений безопасности, функцию зашифрования они берут из большого набора Е функций биективного отображения М в С. По этой причине функции зашифрования и расшифрования имеют метку k. Эта метка k называется ключом и берется из так называемого ключевого пространства K. Набором

Е={ |kЄK} и описывается криптосистема.

Очевидно, что Алиса и Боб должны использовать один и тот же ключ k. Чтобы установить общий ключ, они используют защищенный канал, линию связи, которая не прослушивается. Одним из способов выбора общего ключа является предварительная договоренность, другой заключается в том, что один из участников отправляет ключ другому при помощи некоторого связного. Сегодня для этой цели часто используется криптография с открытым ключом.

Обычно одна и та же криптосистема Е может использоваться в течение долгого времени большим количеством людей, поэтому нужно допустить, что эта криптосистема известна также криптоаналитику. Конфиденциальность данных должна обеспечиваться частой сменой ключа.

Часто бывает так, что М=С, в этом случае хотелось бы, чтобы пары открытый текст-шифртекст при зашифровании на разных ключах были постоянными. В таком случае шифртекст не давал бы никакой информации об открытом тексте (см. теорию информации).

Противник, прослушивающий канал, по которому идет передача данных, может быть двух типов:

· Пассивный (прослушивающий): криптоаналитик пытается вычислить открытый текст m (а еще лучше – ключ k) по шифртексту.

· Активный (взламывающий): криптоаналитик пытается активно воздействовать на передаваемые данные. Например, пытается изменить передаваемый шифртекст.

Чтобы не позволить противнику понять, как легитимные участники передачи данных выработали свой общий ключ, нужно выполнять следующие условия:

Условие 1. Все ключи должны быть равновероятными и всегда выбираться из ключевого пространства случайным образом.

Часто предполагают, что все детали используемого отправителем и получателем криптоалгоритма известны противнику, кроме конкретного значения секретного ключа.

Условие 2 (известное, как условие Керкхоффса). Противник знает все детали алгоритмов зашифрования и расшифрования, кроме конкретного значения секретного ключа.

Также на основе этой теории были предложены схемы с замещением-перестановкой

Теоремы Шеннона

Теорема 1 (К. Шеннон). Для любых ε >0 и δ >0 можно найти такое n, что для любого n > последовательности из V распадаются на два непересекающихся класса В и так, что

Пусть 0 < ε< 1, - произвольное малое число. Пусть все последовательности длины n расположены в порядке убывания вероятностей их появления. Как отмечалось выше, множество открытых сообщений моделируется начальным участком таких последовательностей. Обозначим через β(ε) - число наиболее вероятных последовательностей таких, что сумма их вероятностей ≥ 1-ε, а сумма вероятностей любого набора из (β(ε) - 1) этих последовательностей < 1-ε. Следующая теорема показывает, что при n→ ∞ множество последовательностей, составляющих в нашей модели открытый текст, не зависит от ε.

Теорема 2 (К. Шеннон).Для любого ε >0

Криптографическая стойкость (или криптостойкость) — способность криптографического алгоритма противостоять криптоанализу. Стойким считается алгоритм, который для успешной атаки требует от противника недостижимых вычислительных ресурсов, недостижимого объёма перехваченных открытых и зашифрованных сообщений или же такого времени раскрытия, что по его истечении защищенная информация будет уже не актуальна, и т. д. В большинстве случаев криптостойкость нельзя математически доказать, можно только доказать уязвимости криптографического алгоритма.

Абсолютно стойкие системы

Доказательство существования абсолютно стойких алгоритмов шифрования было выполнено Клодом Шенноном и опубликовано в работе «Теория связи в секретных системах».Там же определены требования к такого рода системам:

· ключ генерируется для каждого сообщения (каждый ключ используется только один раз)

· ключ статистически надёжен (то есть вероятности появления каждого из возможных символов равны, символы в ключевой последовательности независимы и случайны)

· длина ключа равна или больше длины сообщения

· исходный (открытый) текст обладает некоторой избыточностью (что является критерием оценки правильности расшифровки)

Стойкость этих систем не зависит от того, какими вычислительными возможностями обладает криптоаналитик. Практическое применение систем, удовлетворяющих требованиям абсолютной стойкости, ограничено соображениями стоимости и удобства пользования.

Некоторыми аналитиками утверждается, что Шифр Вернама является одновременно абсолютно криптографически стойким и к тому же единственным[источник не указан 1701 день] шифром, который удовлетворяет этому условию.

Достаточно стойкие системы

В основном в криптографических системах гражданского назначения применяются практически стойкие или вычислительно стойкие системы. Стойкость этих систем зависит от того, какими вычислительными возможностями обладает криптоаналитик. Практическая стойкость таких систем базируется на теории сложности и оценивается исключительно на какой-то определенный момент времени и последовательно c двух позиций:

· вычислительная сложность полного перебора

· известные на данный момент слабости (уязвимости) и их влияние на вычислительную сложность.

В каждом конкретном случае могут существовать дополнительные критерии оценки стойкости.

Тема 2