Ймовірнісний підхід до оцінювання ризику

Для кількісного визначення величини ризику, необхідно знати всі можливі наслідки якої-небудь окремої події і ймовірність її настання. Під ймовірністю слід розуміти можливість отримання певного результату. Щодо економічних задач методи теорії ймовірностей зводяться до визначення ймовірності настання події і до вибору з можливих подій найоптимальніших (найраціональніших) подій (результатів, рішень, проектів, стратегій).

Ймовірність настання події може бути визначена об’єктивним і суб’єктивним методами.

Об’єктивний метод визначення ймовірності базується на обчисленні частоти, з якою відбувається подія (статистична ймовірність). Припустимо відомо, що при вкладенні капіталу в який-небудь захід прибуток в сумі 20 тис. грн. отримано в 40 випадках із 100, тоді ймовірність отримання такого прибутку дорівнює 0,4:

,

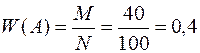де А – випадкова подія, яка полягає у тому, що при вкладанні капіталу в захід буде отримано прибуток в сумі 20 тис. грн.; М – число всіх фактичних появ події А; N – число усіх випадків вкладень капіталу.

Ця ймовірність є об’єктивною, тому що вона визначена на підставі фактичних даних.

Якщо не існує подібної статистики в минулому, тоді неможливо розрахувати ймовірність об’єктивним методом і необхідними є суб’єктивні критерії.

Суб’єктивна ймовірність є припущенням щодо певного результату. Це припущення базується на міркуваннях або особистому досвіді експерта з оцінки. Коли ймовірність визначається суб’єктивно, то різні люди можуть встановлювати різне її значення для однієї і тієї ж події і, таким чином, робити різний вибір. Наприклад, якщо певний захід має проводитися перший раз у відповідному районі, тоді суб’єктивній ймовірності можна надати занадто велике значення. Різна інформація або різні можливості оперувати з однією і тією ж інформацією можуть пояснити, чому суб’єктивні ймовірності варіюють.

Як об’єктивна, так і суб’єктивна ймовірності використовуються при визначенні показників абсолютного та відносного вимірювання ризику.