Ризик у відносному виразі
У відносному виразі ризик визначається, наприклад, як величина можливих збитків, віднесена до деякої бази, за яку найзручніше приймати або майно підприємця, або загальні витрати ресурсів на відповідний вид підприємницької діяльності, або ж сподіваний дохід (прибуток) від конкретного підприємництва.
Для підприємства (корпорації) за базу визначення відносної величини ризику беруть вартість основних фондів та обігових засобів або планові сумарні затрати на вказаний вид ризикової діяльності, маючи на увазі як поточні затрати, так і капіталовкладення чи розрахунковий дохід тощо.
Співвідношення максимально можливого обсягу збитків та обсягу власних фінансових ресурсів інвестора є мірою (оцінкою) ризику, що веде до банкрутства. Ризик вимірюється за допомогою коефіцієнта:
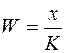 , (11.8)
, (11.8)
де W – коефіцієнт ризику; х – максимально можливий обсяг збитків (грн.); K – обсяг власних фінансових ресурсів із врахуванням точно відомих надходжень коштів (грн.).
Дослідження ризикових заходів дозволяє зробити висновок, що оптимальний коефіцієнт ризику складає 0,3, а коефіцієнт ризику, який веде до банкрутства інвестора, – 0,7 і більше.
Приклад 11.3. Досвідчений інвестор запланував 50 тис. грн. вкласти в перспективні, на його думку, акції під 25 % річних з надією отримати 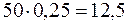 тис. грн. Коли ці акції почали різко падати, він їх продав, понісши 30 % збитків, тобто його втрати становили
тис. грн. Коли ці акції почали різко падати, він їх продав, понісши 30 % збитків, тобто його втрати становили 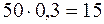 тис. грн. Коефіцієнт ризику для нього
тис. грн. Коефіцієнт ризику для нього 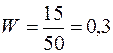 .
.
Молодий бізнесмен, маючи своїх 15 тис. грн., бере в борг 35 тис. грн. під 12 % річних і також вкладає всі 50 тис. грн. в ці акції. Він планує отримати 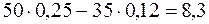 тис. грн. Але в результаті тих же операцій він поніс збитки рівні
тис. грн. Але в результаті тих же операцій він поніс збитки рівні 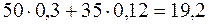 тис. грн. Для нього ці втрати – повне банкрутство. Коефіцієнт ризику для нього
тис. грн. Для нього ці втрати – повне банкрутство. Коефіцієнт ризику для нього 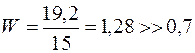 , що теж говорить про банкрутство. Цей приклад підтверджує, що ставка на власний капітал є менш ризиковою. ♦
, що теж говорить про банкрутство. Цей приклад підтверджує, що ставка на власний капітал є менш ризиковою. ♦
У відносному виразі ризик також вимірюють за допомогою коефіцієнта варіації. Він є відношенням стандартного відхилення до середнього сподіваного значення:
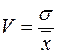 . (11.9)
. (11.9)
Коефіцієнт варіації – відносна величина, тому на його розмір не впливають абсолютні значення досліджуваного показника. З допомогою цього показника можна порівнювати навіть коливання показників, виражених в різних одиницях виміру. Діапазон зміни V від 0 до 1. Чим більший коефіцієнт, тим більший розкид значень показників і тим ризикованішим є оцінюваний проект.
Встановлена така якісна шкала різних коефіцієнтів варіації:
до 0,1 – слабке коливання;
0,1–0,25 – помірне;
понад 0,25 – високе.
Відповідно, чим вище коливання, тим більший ризик.
Якщо, наприклад, у двох альтернативних проектів А і Б виявиться, що VA<VБ, то перевагу слід надати проекту А, який обтяжений меншим ризиком.
Для випадку 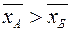 та
та 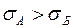 , або
, або 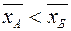 та
та 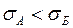 , і при цьому VA=VБ, треба враховувати схильність (несхильність) суб’єкта приймати ризиковані рішення.
, і при цьому VA=VБ, треба враховувати схильність (несхильність) суб’єкта приймати ризиковані рішення.
В неокласичному підході до оцінювання ризику за аналогією з коефіцієнтом варіації існує коефіцієнт семіваріації:
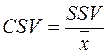 , (11.10)
, (11.10)
де SSV – семіквадратичне відхилення.
Коефіцієнт семіваріації у ряді випадків дозволяє краще оцінити ступінь ризику. Це доцільно, зокрема, тоді, коли зовнішнє економічне середовище, фактори ризику, характерні для аналізованого проекту, відзначаються динамізмом.
Таким чином, система показників кількісної оцінки ризику включає абсолютні і відносні величини (табл. 11.1).
Таблиця 11.1.
Система показників кількісної оцінки ризику
| Показник | Формула |
| Абсолютне вимірювання ризику | |
| Абсолютна величина ризику | 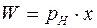 ,
де ,
де 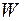 – величина ризику; – величина ризику; 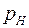 – ймовірність небажаних наслідків, – ймовірність небажаних наслідків, 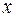 – величина цих наслідків – величина цих наслідків
|
Продовження табл. 11.1
| Середнє сподіване значення (математичне сподівання) | 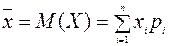 ,
де ,
де 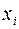 – значення і-го результату; – значення і-го результату;
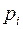 – ймовірність настання і-го результату – ймовірність настання і-го результату
|
| Дисперсія (варіація) | 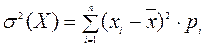
|
| Стандартне відхилення (середньоквадратичне відхилення) | 
|
| Семіваріація | 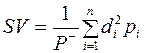 ,
де ,
де 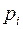 – ймовірність настання і-го результату; – ймовірність настання і-го результату;
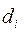 – від’ємні відхилення дійсних результатів від середнього сподіваного, тобто – від’ємні відхилення дійсних результатів від середнього сподіваного, тобто
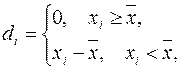
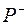 – сума ймовірностей, для яких – сума ймовірностей, для яких 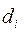 від’ємні від’ємні
|
| Семіквадратичне відхилення | 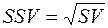
|
| Відносне вимірювання ризику | |
| Коефіцієнт ризику | 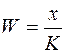 ,
де х – максимально можливий обсяг збитків (грн.);
K – обсяг власних фінансових ресурсів з врахуванням точно відомих надходжень коштів (грн.) ,
де х – максимально можливий обсяг збитків (грн.);
K – обсяг власних фінансових ресурсів з врахуванням точно відомих надходжень коштів (грн.)
|
| Коефіцієнт варіації | 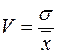
|
| Коефіцієнт семіваріації | 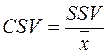
|
Приклад 11.3. Фірма планує вкласти певну частину своїх коштів у розвиток економічної діяльності. Альтернативні варіанти розвитку задано певними стратегіями. Зовнішньоекономічні (з/е) умови, які впливатимуть на показники ефективності кожної стратегії, ймовірні. Виграші за реалізації кожної стратегії та ймовірності зовнішньоекономічних умов наведено в табл. 11.2. Необхідно визначити ефективність і ризикованість кожної стратегії розвитку фірми та зробити висновок, у яку стратегію доцільно вкладати кошти та чому.
Таблиця 11.2
Виграші при реалізації кожної стратегії та ймовірності зовнішньоекономічних умов
| Стратегії, Si | Прибуток за з/е умов | ||||
| S1 | |||||
| S2 | |||||
| S3 | |||||
| S4 | |||||
| S5 | |||||
| Ймовірність з/е умов, Рі | 0,2 | 0,3 | 0,1 | 0,25 | 0,15 |
♦Розв’язування.
1. Визначаємо середню ефективність кожної стратегії за формулою (11.1):
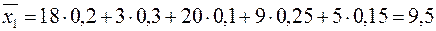 ,
,
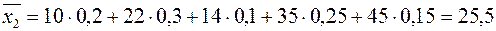 ,
,
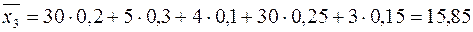 ,
,
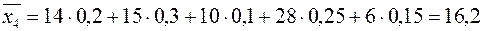 ,
,
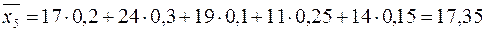 .
.
Оскільки ми знаємо, що чим більша середня ефективність стратегії, тим вигідніша стратегія, то бачимо, що друга стратегія має найбільшу середню ефективність і є найвигіднішою, а решта стратегій найменш ефективні.
2. Кількісна оцінка ризикованості кожної стратегії на основі показників варіації:
а) за дисперсією проводимо розрахунки за формулою (11.3):
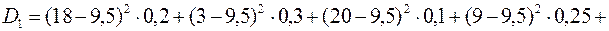
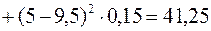 ,
,
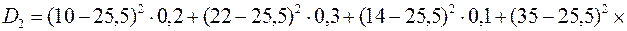
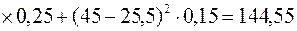 ,
,
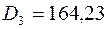 ,
, 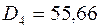 ,
, 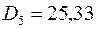 .
.
Дисперсія є одним з абсолютних показників кількісної оцінки ризику. Чим більша дисперсія, тим більший ризик, притаманний стратегії. Виходячи з цього, п’ята стратегія характеризується меншим ризиком, ніж решта стратегій, тобто за цим показником п'ята стратегія є вигіднішою;
б) на основі стандартного відхилення проводимо розрахунки за формулою (11.4):
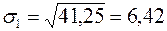 ,
,
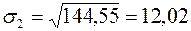 ,
,
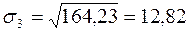 ,
,
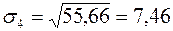 ,
,
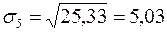 .
.
Стандартне відхилення – це середнє лінійне відхилення від фактичного значення прибутку, чим менше σ, тим надійніша стратегія. Тож за цим показником найвигіднішою є п’ята стратегія;
в) на основі коефіцієнта варіації обчислення проводимо за формулою (11.9):
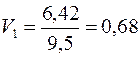 ,
, 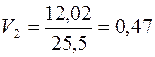 ,
, 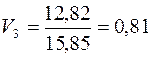 ,
, 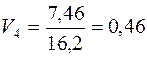 ,
, 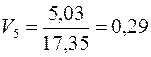 .
.
Чим більше значення коефіцієнта варіації, тим ризикованішою та менш ефективною є стратегія. За цим показником вигідніша п’ята стратегія. Проте коливність її висока;
г) за семіваріацією.
Обчислюємо відхилення прибутку від середньої ефективності за з/е умов і заносимо в табл. 11.3.
За формулою (11.6) додатні відхилення замінимо числом 0, а від’ємні залишаємо, як показано в табл. 11.4.
Далі обчислюємо семіваріацію за формулою (11.5):
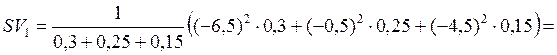
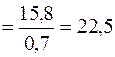 ,
,
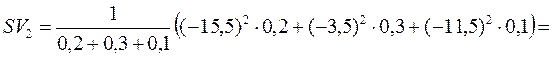
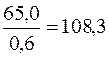 .
.
Таблиця 11.3
| Стратегії, Si | Відхилення прибутку від середньої ефективності за з/е умов, 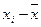
| 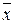
| ||||
| S1 | 8,5 | –6,5 | 10,5 | –0,5 | –4,5 | 9,5 |
| S2 | –15,5 | –3,5 | –11,5 | 9,5 | 19,5 | 25,5 |
| S3 | 14,15 | –10,85 | –11,85 | 14,15 | –12,85 | 15,85 |
| S4 | –2,2 | –1,2 | –6,2 | 11,8 | –10,2 | 16,2 |
| S5 | –0,35 | 6,65 | 1,65 | –6,35 | –3,35 | 17,35 |
| Ймовірність з/е умов, Рі | 0,2 | 0,3 | 0,1 | 0,25 | 0,15 |
Таблиця 11.4
| Стратегії, Si | Від’ємні відхилення прибутку від середньої ефективності за з/е умов, 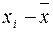
| ||||
| S1 | –6,5 | -0,5 | -4,5 | ||
| S2 | –15,5 | –3,5 | –11,5 | ||
| S3 | –10,85 | –11,85 | –12,85 | ||
| S4 | –2,2 | –1,2 | –6,2 | –10,2 | |
| S5 | –0,35 | –6,35 | –3,35 | ||
| Ймовірність з/е умов, Рі | 0,2 | 0,3 | 0,1 | 0,25 | 0,15 |
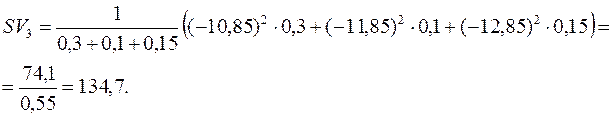
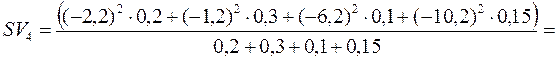
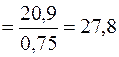 .
. 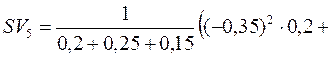
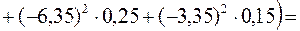
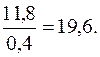
Семіваріація характеризує середні квадратичні відхилення тих значень прибутку, які менші за нього. Чим менша семіваріація, тим менші прогнозовані втрати. За цим показником вигіднішою є також п’ята стратегія;
д) за семіквадратичним відхиленням.
Обчислення проводимо за формулою (11.7):
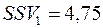 ,
, 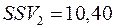 ,
, 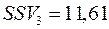 ,
, 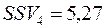 ,
, 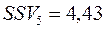 .
.
Отже, вигіднішою є також п’ята стратегія;
е) за коефіцієнтом семіваріації.
Обчислення проводимо за формулою (11.10):
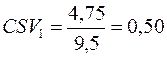 ,
, 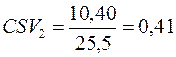 ,
, 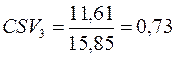 ,
,
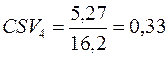 ,
, 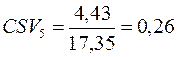 .
.
За цим показником вигіднішою є також п’ята стратегія.
Таким чином, в аналізованому прикладі за абсолютними й відносними показниками найменш ризикованою є п’ята стратегія. ♦
Приклад 11.4. Відомо, що акції виду А та В, залежно від стану економіки, можуть мати різну дохідність. Спеціалісти з економічних досліджень вказали на п’ять можливих станів економіки та оцінили ймовірності настання цих станів (табл. 11.5). Необхідно провести кількісний аналіз ризику акцій.
Таблиця 11.5
| Стани економічного середовища | Імовірність, р | Дохідність акції, % | |
| А | В | ||
| Значне піднесення | 0,2 | ||
| Незначне піднесення | 0,1 | ||
| Стагнація | 0,3 | ||
| Незначна рецесія | 0,3 | ||
| Значна рецесія | 0,1 | –5 | –3 |
♦Розв’язування.
Обчислимо сподівану дохідність для кожної акції за формулою (11.1):
А: 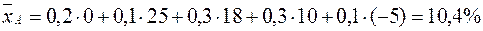 ,
,
В: 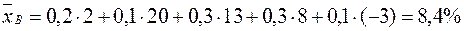 .
.
Для оцінювання ступеня ризику в абсолютному виразі знайдемо дисперсію (варіацію) та середньоквадратичне відхилення за формулами (11.3, 11.4) для кожної з акцій.
Дисперсія дохідності для акції А:
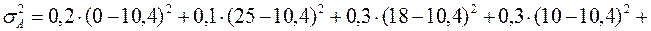
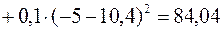 .
.
Тут середньоквадратичне відхилення для акції А буде: 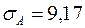 %.
%.
Аналогічно для акції В знаходимо дисперсію:
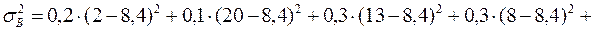
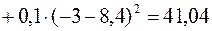
та середньоквадратичне відхилення: 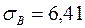 %.
%.
Отже, акція виду А забезпечує вищу сподівану дохідність, ніж акція виду В, але остання менш ризикова за показником середнього квадратичного відхилення. Розраховані коефіцієнти не дають однозначної відповіді щодо вибору кращої за інвестиційною привабливістю акції.
За цією причиною необхідно обчислити ризик у відносному виразі для акцій А та В за допомогою коефіцієнта варіації за формулою (11.9):
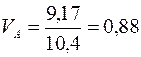 ,
, 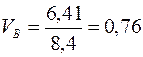 .
.
Отже, акція виду В має краще співвідношення між ризиком та дохідністю, але коливання її високе.
Для більшої переконаності в правильності висновків підрахуємо для обох акцій також показники ступеня ризику, що враховують відхилення від сподіваної дохідності лише в несприятливий бік.
За формулою (11.5) семіваріація для акції А буде:
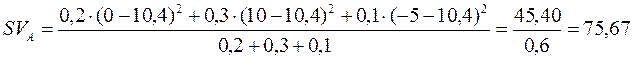 ,
,
а семіквадратичне відхилення за формулою (11.7):
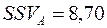 %.
%.
Аналогічні показники для акції В:
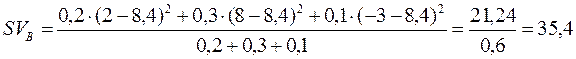 ,
,
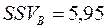 %.
%.
Тепер оцінимо ризик у відносному вираженні для акцій А та В за коефіцієнтом семіваріації, використовуючи формулу (11.10):
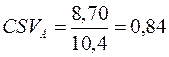 ,
, 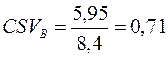 .
.
Отже, прагматичний інвестор обере акцію виду В, адже за всіма відносними показниками ризику вона забезпечує краще співвідношення між ризиком та дохідністю капітальних інвестицій. ♦
Дата добавления: 2014-11-29; просмотров: 6801;
