Ризик в абсолютному виразі
В абсолютному виразі міра ризику може визначатися як добуток ймовірності невдачі (небажаних наслідків) на величину цих небажаних наслідків (збитки, платежі), які мають місце в окресленому випадку:
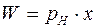 ,
,
де 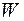 – величина ризику;
– величина ризику; 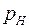 – ймовірність небажаних наслідків;
– ймовірність небажаних наслідків; 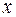 – величина цих наслідків.
– величина цих наслідків.
В окремих випадках, наприклад, у страхуванні, міру ризику визначають як ймовірність настання небажаних наслідків:
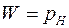 .
.
Середнє сподіване значення (математичне сподівання), пов’язане з невизначеною ситуацією, є середньозваженою всіх можливих результатів, де ймовірність кожного результату використовується як частота або вага відповідного значення:
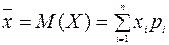 , (11.1)
, (11.1)
де X – економічний показник (дискретна випадкова величина); 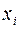 – значення і-го результату;
– значення і-го результату; 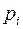 – ймовірність настання і-го результату.
– ймовірність настання і-го результату.
Середнє сподіване значення вимірює результат, який очікується в середньому.
Формула (11.1) застосовується у випадку, коли результати мають певні значення (є дискретною випадковою величиною). Проте коли результати набувають значень з інтервалу 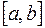 (є неперервною випадковою величиною), середнє сподіване значення обчислюється за формулою:
(є неперервною випадковою величиною), середнє сподіване значення обчислюється за формулою:
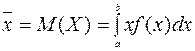 , (11.2)
, (11.2)
де Х – неперервна випадкова величина; 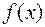 – щільність розподілу ймовірності (диференціальна функція розподілу).
– щільність розподілу ймовірності (диференціальна функція розподілу).
Наприклад, нехай проїзд в тролейбусі становить 60 коп., а штраф за безквитковий проїзд – 12 грн. Якщо ймовірність перевірки квитка 0,1, то сподіване значення результату від безквиткового проїзду 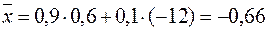 . Таким чином, їздити без квитка за таких умов невигідно. Збитки будуть перевищувати вигоду.
. Таким чином, їздити без квитка за таких умов невигідно. Збитки будуть перевищувати вигоду.
Приклад 11.1.Відомо, що при вкладанні капіталу в варіант А з 150 випадків прибуток 10000 грн. був в 60 випадках (ймовірність 0,4), прибуток 13400 – 78 випадках (ймовірність 0,52), прибуток 28500 грн. – в 12 випадках (ймовірність 0,08). При вкладанні капіталу в варіант Б: прибуток 12500 грн. був в 30 випадках із 120 (ймовірність 0,25), прибуток 14000 грн. – в 54 випадках (ймовірність 0,45), прибуток 25000 грн. – в 36 випадках (ймовірність 0,3). Визначити сподіване значення прибутку за варіантами А та Б.
♦ Розв’язування.
Дані занесемо у таблицю:
| Варіант вкладен-ня капіталу | Ймовірні наслідки | |||||
| імовірність | прибуток | імовірність | прибуток | імовірність | прибуток | |
| А | 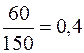
| 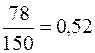
| 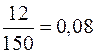
| |||
| Б | 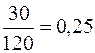
| 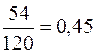
| 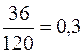
|
Поклавши в основу розрахунків формулу (11.1) сподівані значення прибутків для варіантів А та Б:
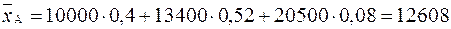 грн.
грн.
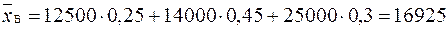 грн.
грн.
Сума сподіваного прибутку для варіанту Б є більшою, ніж для А. На перший погляд можна вибрати варіант Б, оскільки сума сподіваного прибутку є більшою, ніж за А. Але порівнюючи два варіанти, бачимо, що при вкладанні в А величина прибутку коливається від 10000 до 20500 грн., а в Б – від 12500 до 25000 грн. ♦
Середнє сподіване значення є узагальненою величиною, тому для кінцевого вибору варіанта необхідно обчислити коливання (мінливість) можливого результату.
Коливання можливого результату є мірою відхилення сподіваного значення від середньої величини. На практиці застосовують два показники: дисперсію (варіацію) і стандартне відхилення (середньоквадратичне відхилення).
Дисперсія (варіація, 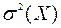 ) є середньою зваженою з квадратів відхилень дійсних результатів від середнього сподіваного. Вона характеризує розсіювання значення випадкового параметра від його середнього прогнозованого значення й обчислюється за формулою:
) є середньою зваженою з квадратів відхилень дійсних результатів від середнього сподіваного. Вона характеризує розсіювання значення випадкового параметра від його середнього прогнозованого значення й обчислюється за формулою:
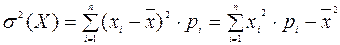 . (11.3)
. (11.3)
Для неперервної величини х на інтервалі 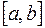 маємо:
маємо:
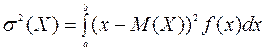 .
.
Стандартне відхилення ( 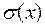 ) дорівнює квадратному кореню з дисперсії:
) дорівнює квадратному кореню з дисперсії:
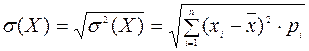 . (11.4)
. (11.4)
Стандартне відхилення показує максимально можливе коливання певного параметра від його середньо сподіваної величини та дозволяє оцінити ступінь ризику з погляду ймовірності його здійснення (чим більша величина числової характеристики, тим ризикованішим є рішення).
Якщо вважати, що є два проекти перший і другий в які можна вкласти кошти і вони у визначений момент в майбутньому забезпечують випадкові величини прибутку, то при відповідних середніх сподіваних значеннях 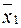 та
та 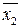 і дисперсіях
і дисперсіях 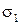 та
та 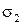 при
при 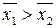 і
і 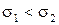 кращим є проект перший.
кращим є проект перший.
В загальному випадку, коли 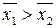 ,
, 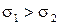 або
або 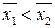 ,
, 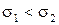 однозначного рішення немає. Інвестор може вибрати проект з більшим сподіваним прибутком, але пов’язаним із великим ризиком, або варіант з меншим сподіваним прибутком, але менш ризикованим. Досліджувану ситуацію можна показати на графіку, де кожен вид вкладень представлено точкою з координатами
однозначного рішення немає. Інвестор може вибрати проект з більшим сподіваним прибутком, але пов’язаним із великим ризиком, або варіант з меншим сподіваним прибутком, але менш ризикованим. Досліджувану ситуацію можна показати на графіку, де кожен вид вкладень представлено точкою з координатами 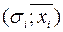 (рис. 11.2.1). Чим більший сподіваний ефект, тим вище розміщена точка, чим більший ризик – тим точка розташована правіше.
(рис. 11.2.1). Чим більший сподіваний ефект, тим вище розміщена точка, чим більший ризик – тим точка розташована правіше.
Очевидно, що досвідчений інвестор віддасть перевагу проекту 1, а не 2 і 3. Також віддасть перевагу проекту 4, а не 2. Проте залежно від схильності до ризику залежить вибір проектів 1, 4 або 5.
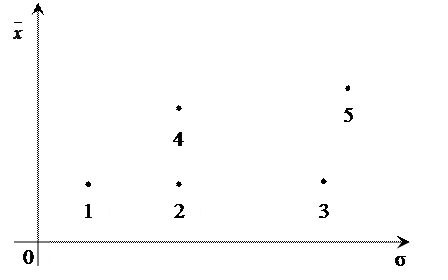
Рис. 11.2.1. Діаграма взаємозв’язку ризику і прибутку
Приклад 11.2.Для даних прикладу 11.1 необхідно оцінити ризик варіантів через дисперсію і стандартне відхилення.
♦Розв’язування.
Визначимо дисперсію і стандартне відхилення за формулами (11.3), (11.4).
Для варіанта А:
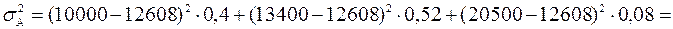 =2720666+4982693+326177=8029536 грн.2
=2720666+4982693+326177=8029536 грн.2
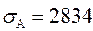 грн.
грн.
Для варіанта Б:
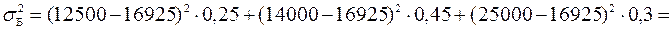 =4895156+3850031+19561688=28306875 грн.2
=4895156+3850031+19561688=28306875 грн.2
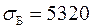 грн.
грн.
Отже, при вкладанні капіталу у відповідні варіанти маємо:
варіант А – 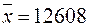 грн.,
грн., 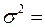 8029536 грн.2,
8029536 грн.2, 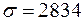 грн.
грн.
варіант Б – 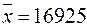 грн.,
грн., 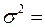 28306875 грн.2,
28306875 грн.2, 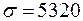 грн.
грн.
Як бачимо, варіант Б має більше сподіване значення прибутку, але він є ризикованішим, ніж А. Який варіант вибрати – це залежить від конкретної людини. Заповзятлива особа віддасть перевагу більшому сподіваному значенню прибутку і стандартному відхиленню, а консервативніша – вибере варіант А. ♦
Підхід, що ґрунтується на використанні дисперсії і стандартного відхилення, вважається класичним. У дисперсії та стандартному відхиленні ризик визначається через відхилення відповідних показників випадкової величини від їхнього середнього сподіваного значення (математичного сподівання). Зауважимо, що за такого визначення міри ризику однаково трактуються як додатні (сприятливі), так і від’ємні (несприятливі) відхилення від 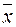 .
.
Проте, якщо існує від’ємне відхилення, тоді відповідне сподіване значення результату нижче від середнього сподіваного. Це означає несприятливу ситуацію. Додатне відхилення водночас вказує на те, що сподіване значення результату вище від середнього сподіваного. Це є сприятлива ситуація для особи, що приймає рішення.
Ризик, насамперед, пов’язаний з несприятливими ситуаціями. За цієї причини за міру ризику часто вибирають семіваріацію (неокласичний підхід до оцінювання ризику). Її обчислюють за формулою:
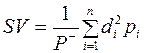 , (11.5)
, (11.5)
де 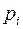 – ймовірність настання і-го результату;
– ймовірність настання і-го результату; 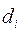 – від’ємні відхилення дійсних результатів від середнього сподіваного, тобто:
– від’ємні відхилення дійсних результатів від середнього сподіваного, тобто:
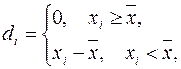 (11.6)
(11.6)
де 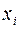 – значення і-го результату;
– значення і-го результату; 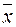 – середнє сподіване значення;
– середнє сподіване значення;
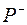 – сума ймовірностей, для яких
– сума ймовірностей, для яких 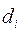 від’ємні.
від’ємні.
Квадратний корінь із семіваріації називається семіквадратичним відхиленням:
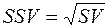 . (11.7)
. (11.7)
Зрозуміло, що чим більшою буде величина 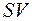 чи
чи 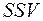 , тим більшим буде ступінь ризику.
, тим більшим буде ступінь ризику.
Дата добавления: 2014-11-29; просмотров: 2252;
