Статистическое распределение выборки

Пусть из генеральной совокупности извлечена выборка, причем х₁ наблюдалось n₁ раз, х₂ – n₂ раз,…, х_k – n_k раз и Sn_i = n – объем выборки.

Наблюдаемые значения x_i называются вариантами, а последовательности вариант, записанные в возрастающем порядке – вариационным рядом.

Число наблюдений n_i называют частотами, а их отношения к объему выборки 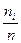= W_i – относительными частотами.

Статистическим распределением выборки называют перечень вариант и соответствующих им частот или относительных частот.

Различают дискретные (возможные значения признака изолированы друг от друга) и интервальные (с непрерывным признаком) распределения.

Составление статистического распределения начинают с определения наименьшего и наибольшего значений признака. Остальные значения записывают между ними в порядке возрастания. Затем подсчитывают частоты каждого значения признака. Для непрерывного варьирующего количественного признака интервал его изменения разбивают на частичные интервалы одинаковой длины (классы). Величина такого интервала (класса) находится по формуле:

,

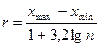где n – объем выборки; x_max – x_min – разность между наибольшим и наименьшим значениями признака. Обычно число классов принимают равным 5-9. Значение признака, находящееся на границе двух интервалов, относят к правой границе интервала.