Понятие функции. Область её определения. Способы задания

К понятию функции приводит изучение разнообразных явлений в окружающем нас мире. Например, каждому значению длины грани куба соответствует его объём; каждому моменту времени в данной местности соответствует определённая температура воздуха; каждому значению возраста животного соответствует его масса; каждому показателю рентабельности соответствует определённая величина прибыли.

Во всех этих примерах общим является то, что каждому числовому значению одной величины сопоставляется определенное числовое значение другой.

Правило f , сопоставляющее каждому числу 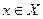единственное число 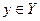, называетсячисловой функцией, заданной на множестве X и принимающей значения во множестве Y.

Если 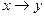, то пишут y = f(x).

Функцией называют также уравнение y = f(x), т.е. формулу, где у выражено через х с помощью правила f.

В уравнении y = f(x) «х» называют независимой переменной или аргументом, а у - зависимой переменной или функциейот «х». Зависимость х и у называется функциональной.

Множество всех значений независимой переменой, для которых определена функция, называетсяобластью определенияэтой функции,обозначается D(f).

Обычно D(f) представляет собой интервал – открытый, полуоткрытый, бесконечный, или их сумму.

Пример. 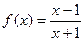. Найти D(f).

Решение. Функция не определена при 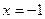. D(f) = (-∞, -1) 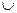(-1, +∞).

Наиболее часто встречаются три способа задания функции: аналитический, табличный, графический.

Аналитический способ: функция задаётся в виде одной или нескольких формул или уравнений.

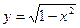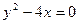Например, 1) , 2) , 3)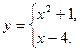

Аналитический способ задания функции является наиболее совершенным, так как к нему приложены методы математического анализа, позволяющие полностью исследовать функцию.

Графический способ: задаётся график функции.

Совокупность точек плоскости xOy, абсциссы которых являются значениями независимой переменной, а ординаты – соответствующими значениями функции, называется графикомданной функции.

Часто графики вычерчиваются автоматически самопишущими приборами или изображаются на экране дисплея. Преимущество графического задания является его наглядность, недостатком – его неточность.

Табличный способ: функция задаётся таблицей ряда значений аргумента и соответствующих значений функции.

Например, таблицы тригонометрических функций, логарифмов, таблицы железнодорожных тарифов.

Табличный способ удобен для использования, он широко применяется при регистрации опытов, лабораторных анализов, при подсчете объема грубых кормов в скирдах и т. д. К недостатку способа относится то, что представление о функциональной зависимости здесь не является полным, так как невозможно поместить в таблице все значения аргумента.

Существует еще один способ задания функции, возникший с развитием и внедрением в производство ЭВМ. Этот способ состоит в указании программы для вычисления значения функций на ЭВМ.