Сущность корреляционного метода анализа и его примен в АХД.

Метод корреляционно-регрессивного анализа широко используется для определения тесноты связи между показателями, не находящимися в функц-ной зависимости. Теснота связи м/д изучаемыми явлениями измеряется корреляционным отношением (для криволинейной зависимости). Для прямолинейной зависимости исчисляется коэфф-т корреляции. Одной из распр-ных аналитических задач, решаемых с применением корреляционно-регрессивного метода, является задача на запуск — выпуск. Допустим, что имеются факт. данные о запуске х и выпуске y изделий. Требуется определить зависимость выпуска изделий в среднем от их запуска, составив соответствующее уравнение регрессии. Значения х и у определяются по формулам:

х = ∑х/n, где n-кол-во запусков, у= ∑ у /n, где n-кол-во выпусков. Дальнейшие вычисления: ∑(х-х)² ; ∑(у- у)² ; ∑(х-х)²*(у- у)² Теснота связи между показателями запуска и выпуска измеряется коэфф-том корреляции, который исчисляется по формуле V= α²xy/αxαy; α_x= √(∑(х-х)²/n) α_y = √(∑(у- у)²/n); α²xy= 1/n ∑(х-х)* (у- у) Считая формулу связи линейной (у = а₀ + а₁х), определим зависимость выпуска изделий от их запуска. Для этого решается система норм-х уравнений, из которой найдем а₀ и а₁.

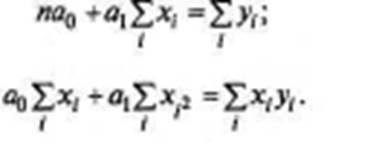
Затем подставляем в формулу связи линейной найденные значения а₀ и а₁ и получаем уравнение регрессии. Корреляционно-регрессивный анализ является одним из наиболее распр-ных математических методов, используемых в АХД. Применение этого метода требует испол-ния программ решения задач на ЭВМ, т.к. корреляционно-регрессивный анализ требует большого количества трудоемких расчетов и большой подготовительной работы. Корреляционный анализ основывается на массовости (не меньше 20 пар наблюдений) данных, так как малое количество наблюдений не позволяет обнаружить закономерность связи. Благодаря корреляционному анализу можно решить две задачи:1. изучается теснота связи между исследуемыми показателями; 2. количественно измеряется степень влияния анализируемого фактора на исследуемый показатель, т. е. проявляется характер связи.