Результаты имитационного эксперимента

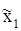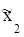Номер серии опыта, J	мм	град	Нормализованное значение факторов	Значение выходной величины в Jℓ-м дублированном опыте, Дж/см3
x1	x2
	0,2		-1	-1	32,6	31,0	33,3	29,7	34,6	31,0	33,3	31,7	31,7	32,1	2,2	32,6
	0,6		+1	-1	19,4	17,3	20,1	19,0	17,3	19,2	19,2	19,0	20,1	18,9	1,1	18,4
	0,2		-1	+1	41,0	38,8	36,9	34,6	37,6	34,6	38,0	36,9	38,8	37,5	4,2	37,7
	0,6		+1	+1	21,4	20,9	22,3	22,3	21,9	21,9	22,8	21,4	23,9	22,1	0,8	22,6

4. Обработанные результаты наблюдений для каждой серии опытов. Определяют средние значения выходного параметра по формуле (2.8)

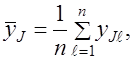
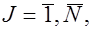
а дисперсии по формуле (2.9)

Подставляя значения выходной величины y_Jℓ (К- удельной работы резания) в приведенные выше выражения, имеем для выборочного среднего

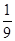= 271,1=32,1, 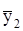= 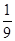169,4=18,8, 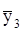= 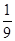337,5=37,5, 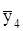= 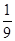198,9=22,1,

для дисперсии

= •17,6=2,2, = •8,5=1,1, = •33,6=4,2, = •6,4=0,8.

Полученные значения заносят в табл. 5.5.

Необходимое количество наблюдений n* для достижения требуемой точности при доверительной вероятности Р=0,95 определяем для серии опытов, в котором дисперсия максимальна или для третей серии .

Пусть максимальная относительная погрешность определителя выходного параметра равна ε=0,05. Тогда по формуле 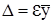максимальная абсолютная погрешность ∆ будет равна: ∆=0,05•37,5=1,9.

Далее проверяют выполнение условия (2.18)

n*₃=2,3²•4,2/1,9²=6,2≤n=9,

где t_{8; 0,05}=2,3 – значение критерия Стьюдента (табл. П.3).

Поскольку условие выполняется, то выбранное первоначальное количество дублированных опытов n=9 является достаточным.

Проверяют однородность дисперсии в различных сериях опытов. По формуле (3.1) определяют расчетное значение критерия Кохрана, G_расч.

G_расч=4,2/(2,2+1,1+4,2+0,8)=0,5

Определяют табличное значение критерия Кохрана, G_табл при принятых: числе степеней свободы f=9-1=8, числе выборок N=4, q=5% уровне значимости. По табл. П.5 Приложения находят G_табл=0,52. Так как G_расч< G_табл, то нулевая гипотеза об однородности дисперсий выборок принимается.

Записывают уравнение регрессии в общем виде, которое позволяет получить матрица планирования (табл. 5.3) выражение (5.17)

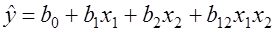
Вычисляют коэффициент регрессии в кодированных значениях факторов по формулам (5.2), (5.3) и (5.4)

b₀=(32,1+18,9+37,5+22,1)/4=27,7,

b₁=[ (-1)32,1+(+1)18,9+(-1)37,5+(+1)22,1]/4=7,2

b₂=[ (-1)32,1+(-1)18,9+(+1)37,5+(+1)22,1]/4=2,2,

b₁₂=[ (+1)32,1+(-1)18,9+(-1)37,5+(+1)22,1]/4=-0,6.

Записывают полученную математическую модель, поставив вместо коэффициентов, записанных в общем виде, их значения

(5.19)

В найденное уравнение регрессии (в кодированных значениях факторов) подставляют значения факторов х₁ и х₂, соответствующих условиям 1-ой, 2-ой,.... n-й серии опытов и определяют значения выходной величины ŷ₁, ŷ₂, ŷ₃ и ŷ₄, предсказанные уравнением регрессии (5.19) для каждой серии опытов

,

,

,

.

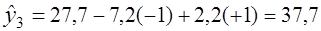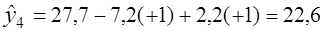Полученные ŷ_J значения заносят в таблицу 5.5.

Вычисляют оценку дисперсий, характеризующую ошибку эксперимента 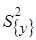по формуле (5.7). Она вычисляется здесь как среднее арифметическое дисперсий серии опытов

.

Вычисляют дисперсии коэффициентов регрессии, характеризующие точность, с которой они найдены. Дисперсии коэффициентов равны друг другу и определяются по формуле (5.8)

или

.

Оценивают значимость коэффициентов регрессии. Оценка значимость коэффициентов регрессии проводится с помощью t-критерия Стьюдента. Для этого определяется:

а) табличное значение t_табл критерия для уровня значимости q=0,05 и числа степеней свободы f_y=N(n-1)=4(9-1)=32 по табл. П.3, t_табл=2,04.

б) для каждого коэффициента регрессии b_i вычисляют расчетное значение t_расч критерия Стьюдента из выражения (5.9)

,

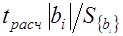где - среднее квадратическое отклонение коэффициента, ;

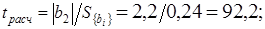
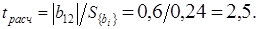
Сравнивая полученные расчетные значения t-критерия с табличными приходят к заключению, что они превышают табличное значение, следовательно все коэффициенты являются значимыми.

Окончательно уравнение регрессии можно записать в виде уравнения

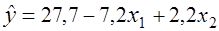(5.20)

Члены уравнения с взаимодействиями исключаем, чтобы осуществить проверку адекватности уравнения (5.18).

5. Выполняют проверку адекватности математической модели (уравнение регрессии 5.18), для этого:

а) вычисляют сумму квадратов разности экспериментального и расчетного значения выходной величины, характеризующую адекватность модели S_ад по формуле (5.13)

,

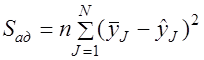откуда

;

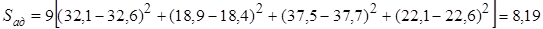б) вычисляют число степеней свободы f_ад, связанное с дисперсной адекватностью по формуле (5.14), f_ад=N-P, где N=4, Р=3

;

в) вычисляют дисперсию адекватности по формуле (5.15)

;

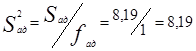г) с помощью f-критерия Фишера при принятом уровне значимости q=0,05 проверяют однородность дисперсии S²_ад=8,19 с числом степеней свободы f_ад=1 и дисперсией, характеризующей ошибку эксперимента S²{y}=2,1 с числом степеней свободы fy=(n-1)N=32. Для этого вычисляют расчетное значение F-критерия Фишера по формуле (5.16)

.

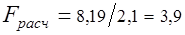Табличное значение F_табл для fy=32 и f_ад=1 по табл. П.6 Приложения составит F_табл=4,2. Поскольку F_расч< F_табл. нулевая гипотеза об однородности дисперсий S²_ад и S²_{y} принимается, полученное уравнение регрессии (5.20) адекватно результатам эксперимента.

Выполняют перевод регрессионного уравнения (5.20) из кодированного вида в натуральный. Это осуществляется путем постановок в него выражени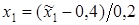й

и ,

тогда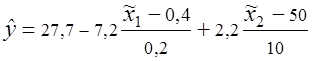

Окончательно после преобразовании, получают уравнение регрессии в натуральных значениях факторов

. (5.21)

6. Анализ результатов эксперимента. Адекватная линейная модель, которой мы располагаем, имеет вид полинома первой степени. Наибольшее влияние на выходную величину (удельную работу резания при продольно-торцовом фрезеровании) оказывает толщина стружки (фактор 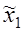), имеющая наибольшее значение коэффициента. При увеличении 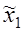значение удельной работы снижается. Наоборот, при увеличении значения фактора (угол встречи) удельная работа возрастает.

Уравнение регрессии позволяет предсказать значение выходной величины для любой точки внутри области варьирования факторов. С его помощью можно строить графики зависимости выходной величины от любого фактора или двух при фиксированных значениях остальных факторов. Постоянная математическая модель может послужить основой для оптимизации процесса или управления процессом.

ВОПРОСЫ КОНТРОЛЬНОГО ЗАДАНИЯ

1. Дайте определение случайной величины.

2. Дайте определение одномерного интегрального и дифференциального закона распределения случайной величины и назовите их свойства.

3. Дайте определение двухмерного интегрального и дифференциального закона распределения случайной величины и назовите их свойства.

4. Укажите числовые параметры, наиболее часто используемые в качестве мер расположения и рассеяния одномерной и двухмерной совокупностей случайных величин.

5. Объясните, каким образом производится построение вариационного ряда, диаграммы накопленных частот, гистограммы выборки одномерной случайной величины.

6. Объясните, каким образом производятся поля рассеяния и составление таблицы распределения двухмерной совокупности случайных величин.

7. Дайте определения генеральной совокупности и выборки.

8. Объясните различия между оцениваемым параметром генеральной совокупности и его оценкой.

9. Объясните, какие оценки параметров распределения называются состоятельными, несмещенными и эффективными.

10. В чем заключается сущность точечных и интервальных оценок параметров.

11. Приведите процедуру нахождения оценок математического ожидания и дисперсии, перечислите их свойства.

12. Приведите процедуру определения доверительных интервалов для математического ожидания, дисперсии и среднего квадратического отклонения.

13. Объясните сущность планирования эксперимента при построении интервальных оценок.

14. Дайте характеристику общей процедуре проверки статистических гипотез.

15. Перечислите, какого рода гипотезы проверяются с помощью критериев значимости и критериев согласия.

16. Оцените процедуру проверки гипотезы относительного значения математического ожидания генеральной совокупности.

17. Опишите процедуру проверки гипотезы относительно значения дисперсии генеральной совокупности.

18. Сформулируйте задачу планирования эксперимента при проверке гипотезы с помощью гипотезы критериев значимости, перечислите примеры ее решения.

19. Опишите процедуру проверки гипотезы о виде функции распределения с помощью χ² (хи – квадрат) Пирсона.

20. Объясните применение таблиц соответствующих распределений при определении доверительных интервалов и проверке гипотез.

21. Дайте определение полного факторного эксперимента (ПФЭ).

22. Дайте определение дробного факторного эксперимента (ДФЭ).

23. Дайте определение фактора. Требования к факторам при планировании. Уровни и интервалы варьирования факторов.

24. Дайте определение параметра оптимизации (выходной величины). Требования к выходной величине при планировании эксперимента.

25. Опишите методику проведения полного факторного эксперимента.

26. Опишите порядок составления матрицы планирования полного факторного эксперимента.

27. Опишите процедуру проверки воспроизводимости вариантов варьирования полного факторного эксперимента.

28. Перечислите, при каких условиях не соблюдается требование воспроизводимости эксперимента и возможные в этом случае решения исследователя.

29. Опишите процедуру проверки значимости оценок коэффициентов регрессии.

30. Укажите, при каких условиях оценки коэффициентов регрессии незначимы и как такие условия исключить.

31. Опишите процедуру проверки адекватности математической модели.

32. Укажите, при каких условиях не соблюдается требование адекватности математической модели и возможные решения в этих случаях.

33. Дайте определение генерирующего соотношения. Как оно выбирается?

34. Дайте определение определяющего соотношения и его использование в составлении системы совместных оценок.

35. Объясните, от чего зависит разрешающая способность дробных реплик.

36. Перечислите преимущества факторного планирования эксперимента пред другими способами проведения активного эксперимента и пассивным экспериментом.

37. Сформулируйте задачу оптимизации.

38. Перечислите подходы решения задачи оптимизации.

39. Выделите общее у всех методов экспериментального поиска экстремума.

40. Опишите сущность и процедуру метода Гауса-Зейделя.

41. Опишите сущность и процедуру метода градиентов.

42. Опишите сущность и процедуру метода крутого восхождения (метод Бокса-Уилсона).

43. Опишите сущность и процедуру симплексного метода.

44. Изложите процедуру статистического анализа результатов в методе крутого восхождения.

45. Чем вызывается необходимость применения метода центрального композиционного планирования (ЦКП).

46. Объясните отличие ЦКП от планирования ПФЭ и ДФЭ.

47. Назовите критерий оптимальности плана при ортогональном и рототабельном ЦКП.

48. Объясните, как достигается ортогональность матрицы планирования при ортогональном ЦКП.

49. Объясните перевод уравнения регрессии для нормализованных величин в уравнение для реальных физических величин.

50. Укажите способ нахождения точек экстремума с помощью полученного математического описания.

51. Элементы теории и методологии научно-технического творчества.

52. Выбор направления научного исследования.

53. Поиск, накопление и обработка научной информации. Информатика как наука.

54. Подобие и моделирование в научных исследованиях.

55. Научные документы и издания.

56. Научно-техническая патентная информация.

57. Основы теории случайных ошибок и методов оценки случайных погрешностей в измерениях.

58. Методы графической обработки результатов измерений.

59. Метрологическое обеспечение экспериментальных исследований.

60. Наука – производительная сила общества. Задачи науки по всемерному внедрению научно-технического прогресса в производство.

61. Организация научно-исследовательской работы в РФ.

62. Система научно-исследовательской работы студентов в высшей школе.

63. Проверка статистических гипотез. Проверка нулевой гипотезы о двух выборочных средних.

64. Методологические основы научного познания. Методы эмпирического познания.

65. Проверка гипотезы нормальности эмпирического распределения.

66. Методологические основы научного познания. Методы теоретического познания.

67. Зависимости между случайными величинами. Проверка гипотезы о некоррелированности случайных величин.

68. Моделирование объектов исследований.

69. Выбор направления научного исследования. Этапы научно-исследовательской работы.

70. Методы обработки экспериментальных данных. Аналитическое выражение результатов измерений (методы подбора эмпирических формул).

71. Метод наименьших квадратов для построения моделей с одной независимой переменной.

72. Научные методы, используемые на эмпирическом и теоретическом уровне познания.

73. Эксперимент. Методология многофакторного эксперимента.

74. Понятие научного знания. Научный метод, классификация методов. Материалистическая диалектика – стратегия метода исследования.

75. Эксперимент. Экспериментальная база. Основы метрологии. Научно-исследовательская работа в деревообработке.

76. Оформление результатов научной работы и передача информации.

77. Внедрение и эффективность научных исследований.

78. Организация работы в научном коллективе.

79. Униформ-рототабельные планы 2-го порядка.

ЛИТЕРАТУРА

1. Пашков В.К. Оформление текстовых документов – Свердловск: РИО УГЛТА, 1990. – 26 с.

2. Пижурин А.А., Розенблит М.С. Исследование процессов деревообработки. – М.: Лесн. пром–ть., 1994, - 232 с.

3. Каменев Б.Б. Основы организации научных исследований: Метод. указ. для спец. 0519. - Л.: ЛТА, 1980. – 55 с.

4. Чубов А.Б., Глушковский А.А. Основы научных исследований.–С. Пб. С-П.: ЛТА, 1992. – 30 с.

5. Глухих В.В. Основы научных исследований: Курс лекций для студентов инженерно-экологического факультета.– Екатеринбург,1998.-90 с.

6. Статистические методы в инженерных исследованиях (лабораторный практикум): Учеб. пособие / Бородюк В.П., Вощинин А.П., Иванов А.З. и др.; Под редакцией Г.К. Круга – М: Высш. шк., 1983. – 216 с.

7. Гмурман В.С. Теория вероятностей и математическая статистика. – М.:: Высш. шк., 1972. – 367 с.

8. Адлер Ю.П., Марков Ю.В., Грановский Ю.В. Планирование эксперимента при поиске оптимальных условий - М.: Наука, 1976. – 279 с.

9. Санев В.И. Обработка древесины круглыми пилами. – М.: Лесн. пром–ть., 1980. – 230 с.