К выполнению работы
5.2.1. Планирование полного факторного эксперимента ПФЭ 2К
Для иллюстрации порядка выполнения раздела и лабораторной работы в целом используем пример задания, приведенного в лабораторной работе № 2 (п. 2.1).
Словесная формулировка задачи. Исследуется зависимость удельной работы резания К, Дж/см3 от толщины стружки а, мм, и угла встречи jв, град., при продольно-торцевом фрезеровании.
Математическая формулировка задачи. Исходные зависимости представлены на рис. 5.1.
 |
Рис. 5.1. Зависимость удельной работы резания К от толщины стружки а и угла встречи jв при продольно-торцевом фрезеровании
Уровни и интервалы варьирования переменных факторов приведены в табл. 5.1
Таблица 5.1
| Уровни факторов | Натуральные значения факторов | Кодированные значения факторов | ||
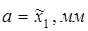
|  град
град
| x1 | x2 | |
| Нижний уровень, xi min | 0,2 | -1 | -1 | |
| Верхний уровень, xi max | 0,6 | +1 | +1 | |
| Основной уровень, xi 0 | 0,4 | |||
| Интервал варьирования, Dxi | 0,2 | - | - |
Постоянные факторы и их уровни: порода – сосна, влажность W=12%, толщина срезаемого слоя h=3 мм, угол резания d=60°, радиус закругления лезвия r=5 мкм и скорость резания V=40 м/с.
Оценочный показатель (выходная величина y) – удельная работа резания К, Дж/см3 (Кºy), диапазон ее изменения К=18.....44 Дж/см3.
В заключение составляют рабочую матрицу планирования ПФЭ 2К, в которую дополнительно включают вектор-столбец со значениями выходной величины у по графикам на рис. 5.1.
Рабочая матрица планирования ПФЭ 2К с дублированными опытами представлена в табл. 5.2
Таблица 5.2
Рабочая матрица ПФЭ 2К с дублированными опытами
 Номер опыта (серии), J Номер опыта (серии), J
| 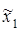 ,
мм ,
мм
| 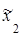 ,
град ,
град
| 
| 
| y=K, Дж/см3 | Значения yJℓ в дублированных опытах | yJ | SJ2 | ŷJ | ||||
| ..... | n-1 | n | |||||||||||
| 0,2 | -1 | -1 | 32,0 | ||||||||||
| 0,6 | +1 | -1 | 19,0 | ||||||||||
| 0,2 | -1 | +1 | 38,0 | ||||||||||
| 0,6 | +1 | +1 | 29,0 |
Значения выходной величины yJℓ в дублированных опытах в табл. 5.2 заполняют по результатам имитационного эксперимента с действительными значениями К=у из графиков на рис. 5.1. Рекомендуется в учебном эксперименте относительную погрешность принимать ε£0,01. Это связано с тем, что совместное влияние ε и случайных чисел на значение yJℓ может значительно превышать принятую в деревообработке погрешность – 0,05. Это может привести к затруднениям при обработке результатов эксперимента. Величина ŷJ определится по результатам ее расчета по уравнению регрессии (математической модели), получение которой является целью эксперимента.
5.2.2. Построение математической модели
Матрица планирования ПФЭ 2К позволяет представить зависимость между выходной величиной и переменными факторами в виде математической зависимости, которая называется уравнением регрессии (выражения (1.5) и (1.6)). Уравнение
 , (5.1)
, (5.1)
являющееся частным случаем уравнения (1.5), называется линейной математической моделью объекта.
 Для составления уравнения регрессии (1.6) помимо выбора его вида необходимо определить коэффициенты bi, i=1, K, которые называются коэффициентами регрессии и определяются по формуле
Для составления уравнения регрессии (1.6) помимо выбора его вида необходимо определить коэффициенты bi, i=1, K, которые называются коэффициентами регрессии и определяются по формуле
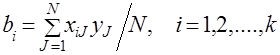 . (5.2)
. (5.2)
Для вычисления коэффициента регрессии bi уравнения (5.1) необходимо вектор-столбец кодированных значений соответствующего фактора умножить на соответствующие значения выходной величины и их алгебраическую сумму разделить на количество серий опытов. Значение b0 определяют по формуле
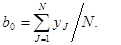 (5.3)
(5.3)
Для облегчения унификации расчетов коэффициентов регрессии с учетом эффектов взаимодействия строят расширенную расчетную матрицу планирования, представленную в табл. 5.3
Таблица 5.3
Расширенная расчетная матрица планирования ПФЭ 2К
| Номер серии (опыта) | x0 | x1 | x2 | x3= x1 x2 | yJ |
| +1 | -1 | -1 | +1 | y1 | |
| +1 | +1 | -1 | -1 | y2 | |
| +1 | -1 | +1 | -1 | y3 | |
| +1 | +1 | +1 | +1 | y4 |
Распишем формулы (5.2) и (5.3) для плана ПФЭ 22 с двумя факторами
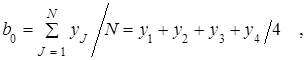


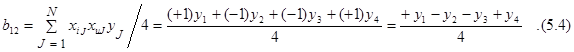
После выбора вида математической модели объекта и построения матрицы планирования переходим к ее реализации.
5.2.3. Проведение эксперимента с равномерным
дублированием опытов
Эксперимент с дублированными опытами – такой эксперимент, когда каждый опыт ПФЭ повторяется (дублируется) некоторое число раз. Например, n. Эксперимент содержит N серий опытов (N=2К), где каждая серия состоит из n опытов, проводимых в одинаковых условиях. Тогда общее количество опытов с учетом дублирования равно Nn.
 Среднее арифметическое дублированных опытов J-ой серии yJ будет равно
Среднее арифметическое дублированных опытов J-ой серии yJ будет равно
 (5.5)
(5.5)
где n – количество дублированных опытов J-й серии;
ℓ=1,2,...,n.
Дублирование опытов позволяет повысить точность определения выходной величины, снизить влияние на точность систематических и случайных ошибок.
Для исключения систематических ошибок, вызванных воздействием неконтролируемых факторов при постановке опытов, запланированных матрицей, их необходимо рандомизировать во времени. Для рандомизации используют таблицы случайных чисел. В случайном месте таблицы выписывают числа с 1 до N, в общем столько, сколько опытов в матрице планирования с отбрасыванием чисел больших N и уже выписанных. Например, для реализации матрицы планирования ПФЭ 2К (табл. 5.3) получилась следующая последовательность: 2, 1, 3, 4. Следовательно, первым реализуется опыт № 2. Затем опыт № 1 и т.д. Выбранную случайным образом последовательность опытов не рекомендуется нарушать.
При имитационном планировании рандомизация достигается выбором относительной погрешности и значением случайного числа. Методика построения имитационного эксперимента изложена в разделе 2.1 лабораторной работы № 2.
5.2.4. Обработка результатов эксперимента
Уравнения регрессии подвергают тщательному статистическому анализу. Цели анализа: извлечение из результатов эксперимента максимума информации; оценка точности и достоверности полученных зависимостей. Обработку результатов эксперимента при равномерном дублировании опытов рекомендуют проводить в следующем порядке:
 а) вычисляют среднее значение yJ для J–го опыта по формуле (2.8);
а) вычисляют среднее значение yJ для J–го опыта по формуле (2.8);
б) вычисляют коэффициенты регрессии по формулам (5.2),(5.3) и (5.4),причем вместо yJ следует взять среднеее значение 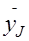 (п.а). Записывают полученную математическую модель (5.1), поставив вместо коэффициентов, записанных в общем виде, их значения;
(п.а). Записывают полученную математическую модель (5.1), поставив вместо коэффициентов, записанных в общем виде, их значения;
в) вычисляют оценки дисперсии S2J для каждой серии опытов по формуле
 (5.6)
(5.6)
где n – число дублированных опытов в серии,
yJℓ - значение выходной величины в ℓ-м дублированном опыте (J=1, 2, ...., N, ℓ= 1, 2, ...., n):
Полученные значения S2J записывают в табл. 5.2.
г) проверить однородность дисперсии опытов S2J по формуле (3.1) по G-критерию Кохрана;
д) вычисляют оценки дисперсий, характеризующих ошибку эксперимента S2íyý по формуле
 (5.7)
(5.7)
Число в знаменателе формулы (5.7) N(n-1)=fy и представляет собой число степеней свободы, связанных с дисперсией S2íyý;
е) вычисляют дисперсии коэффициентов регрессии по формуле
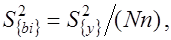 (5.8)
(5.8)
Дисперсии коэффициентов равны друг другу для планов ПФЭ и характеризуют точность, с которой они найдены;
ж) оценивают значимость коэффициентов регрессии с помощью t-критерия Стьюдента, для чего:
- для каждого коэффициента регрессии bi вычисляется расчетное значение критерия Стьюдента tрасч по формуле
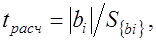 (5.9)
(5.9)
где Síbiý - среднее квадратическое отклонение коэффициента
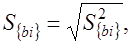 (5.10)
(5.10)
- определяют табличное значение критерия Стьюдента tтабл для уровня значимости q и числа степеней свободы fy по табл. П.3 Приложения
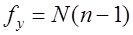 ; (5.11)
; (5.11)
- проверяют условие tрасч£tтабл ; коэффициенты регрессии для которых это условие выполняется являются незначимыми, их можно исключить из математической модели.
и) при отсутствии дублированных опытов ошибку эксперимента оценивают с помощью отдельно проведенной серии дублированных опытов с числом m³120.
Оценка дисперсии, характеризующая ошибку эксперимента в этом случае определяется по формуле
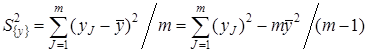 , (5.12)
, (5.12)
к) определяют значения выходной величины ŷ1,...., ŷN, предсказанные уравнением регрессии (5.1). Для этого в уравнение подставляют кодированные значения факторов x1, x2,... xK последовательно для каждой серии опытов и вычисляют значения выходной величины, например, по результатам матрицы плана ПФЭ 22 имеем
ŷ1=b0+(-1)b1+(-1)b2,
ŷ2=b0+(+1)b1+(-1)b2,
ŷ3=b0+(-1)b1+(+1)b2,
ŷ4=b0+(+1)b1+(+1)b2,
а полученные значения записывают в табл. 5.2.
5.2.5. Проверка адекватности математической модели
Проверка достоверности и точности полученной модели называется проверкой ее адекватности результатам эксперимента. Ее выполняют после вычисления и проверки значимости коэффициентов регрессии. Чтобы проверить гипотезу об адекватности результатов эксперимента, найденным из уравнения связи, достаточно оценить отклонения, предсказанные уравнением регрессии выходной величины ŷ от результатов эксперимента у в различных точках факторного пространства.
Такую проверку выполняют в следующем порядке:
а) вычислют сумму квадратов разности средних значений выходной величины, полученных экспериментально и значений, вычисленных по уравнению регрессии (5.1), характеризующую адекватность модели
 , (5.13)
, (5.13)
где n – число дублированных опытов.
б) вычисляют число степеней свободы fад, связанных с дисперсией адекватности; при равномерном дублировании и при отсутствии дублирования fад определяют по формуле
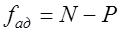 , (5.14)
, (5.14)
где Р – число оцениваемых коэффициентов регрессии (при N=P адекватность модели проверить невозможно).
в) вычисляют дисперсию адекватности S2ад по формуле
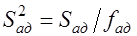 , (5.15)
, (5.15)
г) вычисляют расчетное значение критерия Фишера Fрасч по формуле
 , (5.16)
, (5.16)
д) определяют табличное значение критерия Фишера Fтабл по табл. П.6 Приложения для q=5% уровня значимости и расчетных значений fад из выражения (5.14) и fy из выражения (5.11).
е) проверяют условие Fрасч£Fтабл , если оно выполняется, то уравнение регрессии соответствует результатам опыта или оно адекватно.
В случае невыполнения условия – уравнение регрессии не адекватно и результаты опытов нельзя описать уравнением данного вида. В этом случае нужно в уравнение ввести взаимодействия или перейти к полному уравнению регрессии второго порядка;
ж) перевод регрессионного уравнения (5.1) из кодированного вида в натуральный осуществляют путем подстановки в него выражений (1.3).
5.2.6. Анализ результатов эксперимента
Анализ результатов эксперимента предусматривает интерпретацию модели. Устанавливается, в какой мере каждый из факторов влияет на выходную величину на основании величины и знака коэффициента регрессии. Рассматривается расположение совокупности факторов в ряд по силе их влияния на выходную величину, выясняются факторы не оказывающие существенного влияния на нее. Оцениваются возможности уравнения регрессии для натуральных значений факторов предсказывать: значения выходной величины для любой точки внутри области варьирования факторов; служить основой для оптимизации исследуемого процесса или управления им.
Дата добавления: 2014-12-05; просмотров: 965;
