Составление выборки пар (х, у) случайных величин
 Поле опыта Поле опыта
| х | у, по рисунку | Случайные числа RJℓ | Значения у ℓ-м дублированных опытах | у | ||||||||
| у1 | у2 | у3 | у4 | у5 | |||||||||
| 0,20 | 32,0 | 31,7 | 32,0 | 32,0 | 29,1 | 29,8 | 30,9 | ||||||
| 0,25 | 28,0 | 27,1 | 26,0 | 26,6 | 29,1 | 28,6 | 27,5 | ||||||
| 0,30 | 25,0 | 25,0 | 27,0 | 25,5 | 25,5 | 25,8 | |||||||
| 0,35 | 23,0 | 20,9 | 20,9 | 22,8 | 20,9 | 21,7 | |||||||
| 0,40 | 22,0 | 21,8 | 22,4 | 23,8 | 20,5 | 22,1 | |||||||
| 0,45 | 21,0 | 22,7 | 19,1 | 19,1 | 20,4 | ||||||||
| 0,50 | 20,0 | 20,4 | 21,2 | 19,4 | 20,0 | ||||||||
| 0,55 | 19,5 | 19,3 | 18,5 | 17,7 | 18,5 | 18,9 | 18,6 | ||||||
| 0,6 | 19,0 | 20,5 | 20,5 | 20,1 | 17,7 | 20,1 | 19,8 |
2. Формирование блока случайных чисел для имитационного эксперимента. Блок чисел объемом J k выбирается из табл. П.2 Приложения. Примем количество серий опытов N=9, количество дублированных опытов ℓ в каждой серии n=5. Блок случайных чисел RJℓ Jℓ=9 5, выбранных в случайном месте таблицы случайных чисел, записываем в табл. 4.1 (гр. 4….8).
3. Имитационный эксперимент. Выполняется по методике использованной в разделе 2.1 лабораторной работы № 2 по формуле (2.1). В эксперименте относительную погрешность ε принять равной ε=0,01. Результаты эксперимента по значениям выходной величины у (гр. 3 табл. 4.1) по каждой J-й серии заносим в графы 9….13 табл. 4.1.
4. Определение средних 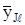 по сериям опытов. Условное среднее
по сериям опытов. Условное среднее 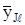 определяются по (2.8.), например, значение
определяются по (2.8.), например, значение 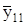 равно.
равно.
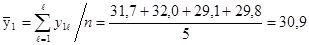 и т.д.
и т.д.
Результаты расчетов условных средних 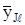 заносим в графу 14 табл. 4.1. Сформируем табл. 4.2 пар (
заносим в графу 14 табл. 4.1. Сформируем табл. 4.2 пар ( 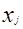 ,
, 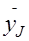 ) наблюдений.
) наблюдений.
Таблица 4.2
Таблица пар ( 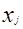 ,
, 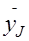 ) случайных величин
) случайных величин
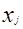
| 0,20 | 0,25 | 0,30 | 0,35 | 0,40 | 0,45 | 0,50 | 0,55 | 0,60 |
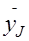
| 30,9 | 27,5 | 25,8 | 21,7 | 22,1 | 20,4 | 20,0 | 18,6 | 19,8 |
5. Построение поля корреляции. На плоскости прямоугольной системы координат по оси абсцисс откладывают значения х (а, мм), ординат – значения 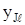 и
и 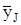 (k, Дж/см3) по данным табл. 4.1 и 4.2. Для облегчения анализа рекомендуется весь массив точек с координатами xJ,
(k, Дж/см3) по данным табл. 4.1 и 4.2. Для облегчения анализа рекомендуется весь массив точек с координатами xJ, 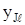 обвести замкнутым контуром. Характер этого контура помогает сделать более точные выводы корреляционного анализа. Через точки с координатами условных средних проводим линию регрессии. Результаты имитационного эксперимента представлены на рис.4.1.
обвести замкнутым контуром. Характер этого контура помогает сделать более точные выводы корреляционного анализа. Через точки с координатами условных средних проводим линию регрессии. Результаты имитационного эксперимента представлены на рис.4.1.
 |
Рис. 4.1. Поле корреляционной зависимости удельной силы резания от толщины стружки а для угла встречи jв=40°
Анализ поля корреляции (рис 4.1) позволяет сделать следующие предварительные выводы:
а) имеется зависимость удельной работы резания от толщины стружки при продольно-торцевом фрезеровании;
б) зависимость является корреляционной экспоненциальной;
в) знак зависимости отрицательный – увеличение толщины стружки приводит к снижению удельной работы резания (условной средней 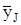 );
);
г) зависимость является тесной.
6. Проверка нуль-гипотезы о некоррелированности величин х,у. Процедура проверки включает предварительный расчет выборочного коэффициента корреляции r по формуле (4.2). Удобно для расчета подготовить таблицу по образцу табл. 4.3.
Таблица 4.3
Расчет коэффициента корреляции
| Номер серии, J | хJ | yJ | хJ yJ | хJ2 | yJ2 |
| 0,20 | 30,9 | 6,08 | 0,04 | 955,0 | |
| 0,25 | 27,5 | 6,88 | 0,06 | 756,3 | |
| 0,30 | 25,8 | 7,74 | 0,09 | 665,6 | |
| 0,35 | 21,7 | 7,60 | 0,12 | 470,9 | |
| 0,40 | 22,1 | 8,84 | 0,16 | 488,4 | |
| 0,45 | 20,4 | 9,18 | 0,20 | 416,2 | |
| 0,50 | 10,00 | 0,25 | 400,0 | ||
| 0,55 | 18,6 | 10,23 | 0,30 | 346,0 | |
| 0,6 | 19,8 | 11,88 | 0,36 | 392,0 |
В графу 1 табл.4.3 заносят номера серии опытов, в графы 2 и 3 соответственно значения хJ и yJ из табл.4.2. В графу 4 заносят значения произведений 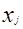
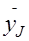 , а в графы 5 и 6 соответственно квадраты случайных величин хJ2 и yJ2.
, а в графы 5 и 6 соответственно квадраты случайных величин хJ2 и yJ2.
Затем определяют суммы:
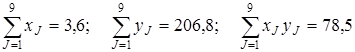
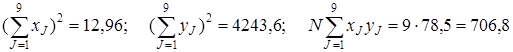 ;
;
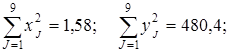
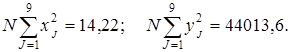
Воспользовавшись значениями рассчитанных сумм по данным табл. 4.3 вычисляют по формуле 4.2 выборочный коэффициент корреляции r
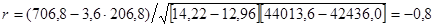 .
.
Выполняем проверку нуль-гипотезы о некоррелированности величин х, у:
а) определяют расчетное значение t-критерия Стьюдента tрасч по формуле (4.3)
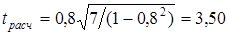 ;
;
б) определяют по табл. П.3 табличное значение t-критерия для уровня значимости q=5% и числа степеней свободы f=N-2=9-2=7; tтабл =2,36;
в) проверяем условие некоррелированности tрасч> tтабл (3,50>2,36), следовательно нуль-гипотеза отвергается, а между случайными величинами существует корреляционная связь (r≠0).
Совместный анализ поля корреляции и значения выборочного коэффициента парной корреляции r позволяет утверждать, что:
а) имеется зависимость удельной работы резания от толщины стружки;
б) данная зависимость является корреляционной линейной;
в) знак зависимости – отрицательный;
г) зависимость является тесной.
Лабораторная работа № 5
Дата добавления: 2014-12-05; просмотров: 881;
