Ход решения. 1. Заключаем прямую l во вспомогательную плоскость частного положения

1. Заключаем прямую l во вспомогательную плоскость частного положения. Линией пересечения плоскости с гранной поверхностью будет ломаная линия. Заключаем прямую l во фронтально-проецирующую плоскость α^π₂, l₂Î α₂ (рис. 32).

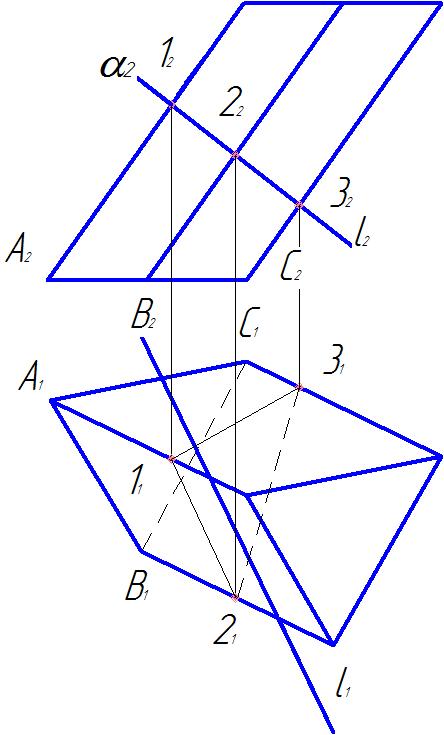
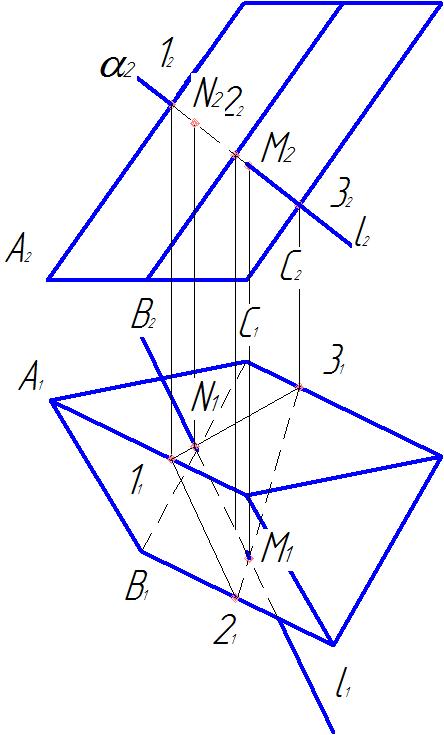
Рис.32 Рис.33

2. Строим линию пересечения плоскости α с призмой. Отметим 1₂, 2₂, 3₂ на α₂.

3. Построим горизонтальные проекции 1₁, 2₁ и 3₁ на соответствующих ребрах.

4. Соединяем горизонтальные проекции1₁-2₁-3₁ломаной линией с учетом видимости.

5. На пересечении горизонтальной проекции l₁ с горизонтальной проекцией 1₁-2₁-3₁ отметим горизонтальные проекции M₁ и N₁искомых точек М и N.

6. Построим фронтальные проекции M₂ и N₂ точек М и N на l₂.

7. Определяем видимость прямой l. Между полученными точками M и N прямая невидима всегда. Горизонтальная проекция l₁ невидима между M₁N₁ и от M₁ до горизонтальной проекции ребра В₁, т. к. горизонтальная проекция М₁ принадлежит невидимой относительно π₁ грани ВС.

На π₂: точка М лежит на грани BС видимой относительно π₂, следовательно, М₂ видима и фронтальная проекция l₂ видима до М₂. Точка N принадлежит грани А C, невидимой относительно π₂, следовательно, фронтальная проекция N₂ не видима и фронтальная проекция l₂ от N₂ невидима. За очертаниями призмы прямая l видима (рис. 33).

Задача 9.Построить три проекции геометрического тела с вырезом. Выполнить задачу 9 на формате А3.

Пример 1. Вырез на конусе (рис. 34).

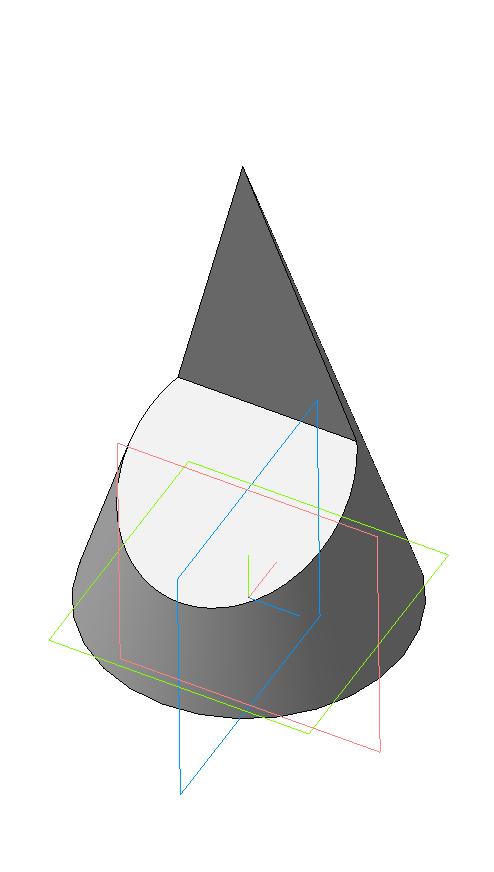
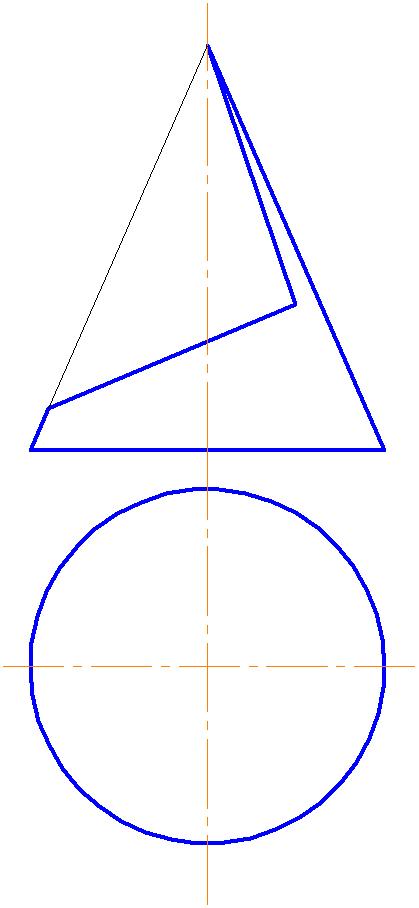
Рис. 34

Вырез произведен двумя плоскостями. Одна проходит через вершину конуса и рассечет его поверхность по образующим. Вторая плоскость – фронтально-проецирующая, линия пересечения – часть эллипса, ограниченная прямой принадлежащей линии пересечения плоскостей.