Ход решения. 1. Отметим характерные точки линии пересечения

1. Отметим характерные точки линии пересечения. Точки А и В лежат на пересечении фронтальных очерков. Точки С и D найдем на пересечении экватора сферы a и окружности b поверхности конуса, лежащих в одной горизонтальной плоскости α. Аналогично могут быть найдены и другие точки линии пересечения. Так точки М и N строим как пересечение окружностей c и d, принадлежащих одной горизонтальной плоскости β (рис.47).

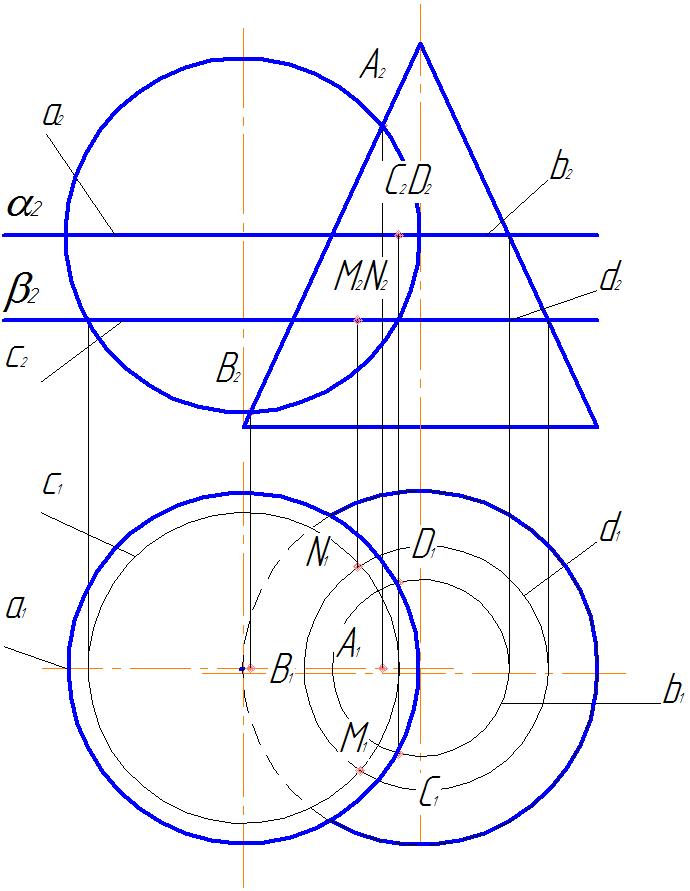
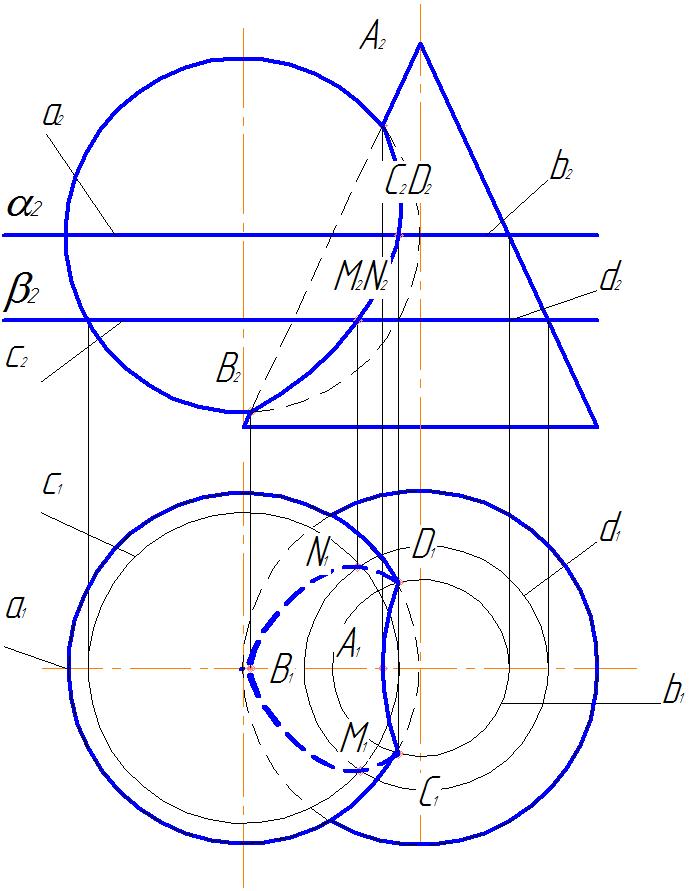
Рис. 47 Рис. 48

3. Полученные точки соединяем плавной кривой с учетом видимости. При установлении видимости следует помнить, что эта линия будет видима, если она принадлежит как поверхности сферы, так и конуса. Точки А и В отделяют видимую относительно фронтальной плоскости часть линии пересечения (она проходит через точки А, С, М, В) от невидимой. В данной задаче фронтальные проекции видимой и невидимой части линии пересечения совпадают.

Точки С и D отделяют видимую относительно горизонтальной плоскости часть линии пересечения от невидимой. Точка А видима относительно горизонтальной плоскости проекций, так как лежит выше экватора сферы. Следовательно линия, проходящая через точки А, С, D – видима, остальная часть линии невидима. Определим видимость очерков поверхности конуса и сферы (рис. 48).

Задача 11.Определить расстояния от точки А до прямой l (рис. 49)

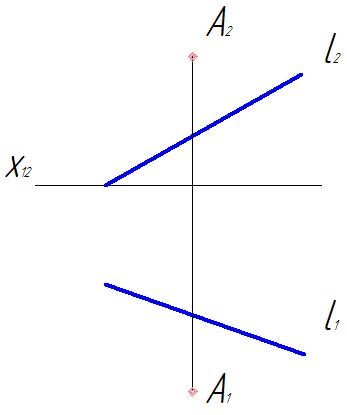
Рис. 49

Расстояние от точки до прямой определяется длиной отрезка перпендикуляра, опущенного из точки на прямую.