Ход решения. 1. Плоскость π4 будет перпендикулярна к плоскости α, если она перпендикулярна к горизонтали этой плоскости

1. Плоскость π₄ будет перпендикулярна к плоскости α, если она перпендикулярна к горизонтали этой плоскости. При этом ось х₁₄ перпендикулярна к горизонтальной проекции h₁ горизонтали h плоскости α. Дополнительной ортогональной проекцией плоскости α на плоскость π₄ является прямая B₄C₄D₄ (рис.52 ).

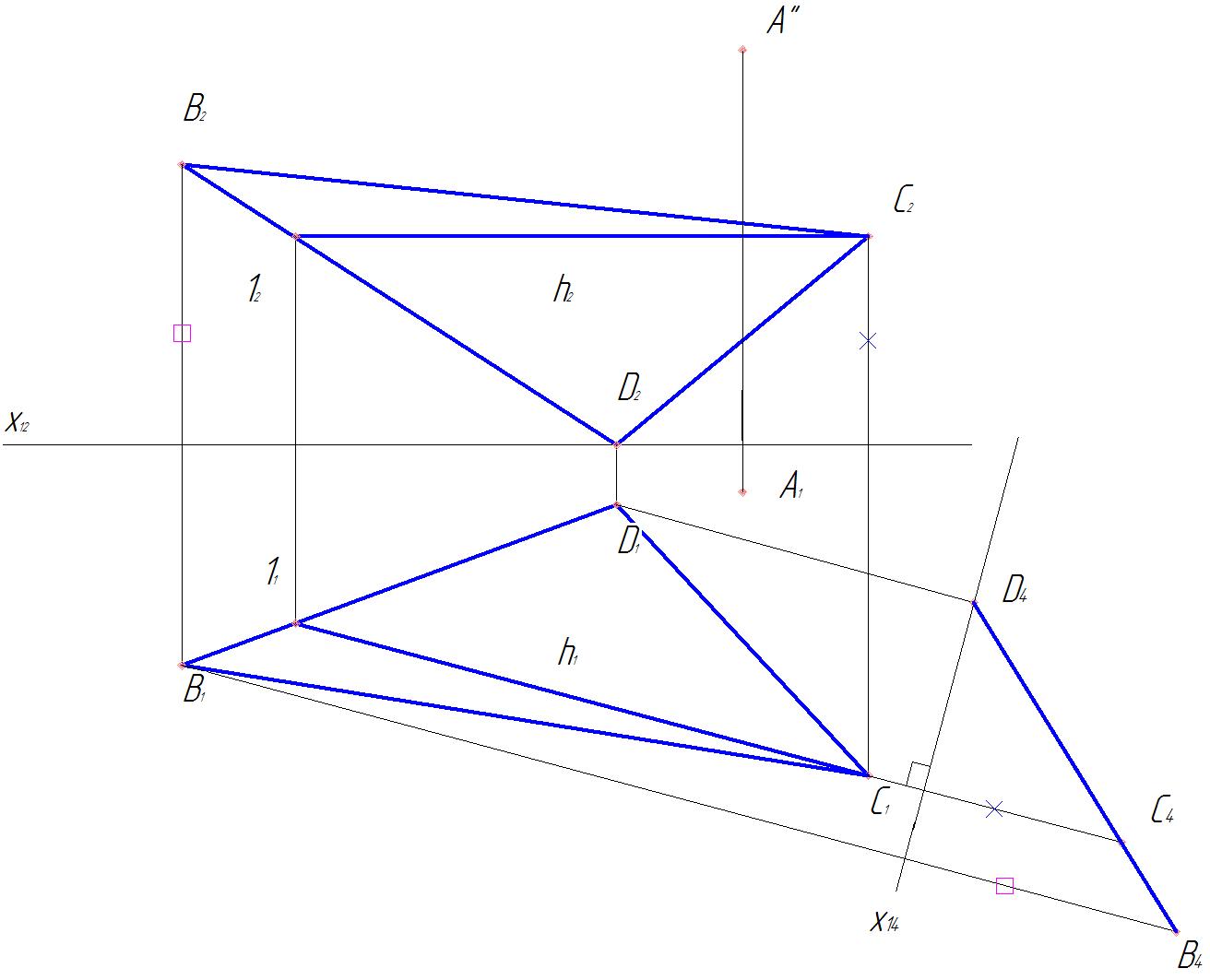
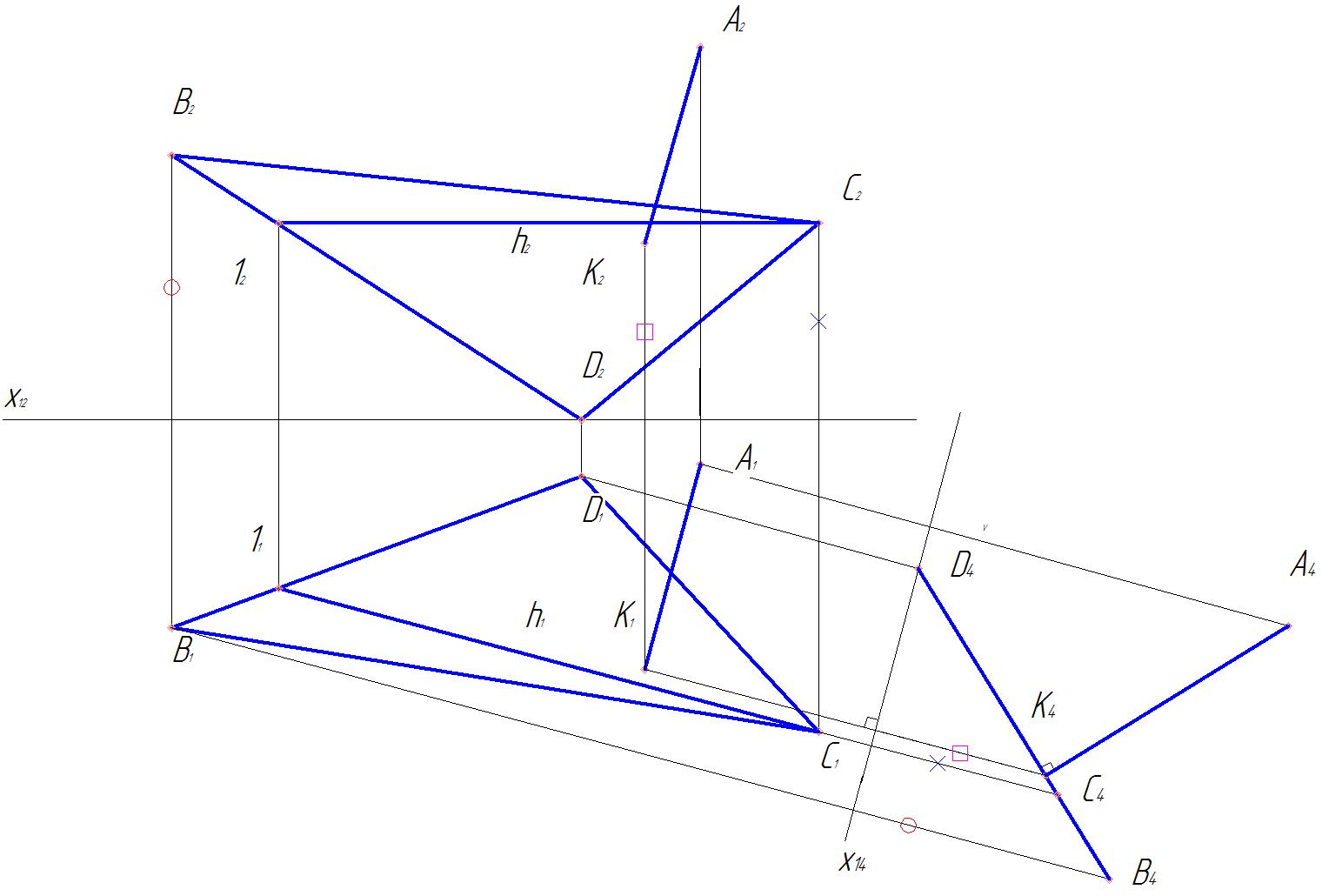
Рис. 52 Рис.53

2. Из точки А₄ опускаем перпендикуляр А₄ K₄ на прямую B₄C₄D₄. Длина отрезка А₄K₄ равна расстоянию от точки А до плоскости α(ΔBCD) (рис.53 ).

Построим проекции отрезка АК. Горизонтальная проекция А₁К₁ параллельна оси х₁₄, так как отрезок АК параллелен плоскости π₄, и перпендикулярна к горизонтальной проекции h₁горизонтали h плоскости α. Фронтальную проекцию К₂ точки К строим по двум ее проекциям К₁ и K₄.

На основании решения рассмотренной задачи можно определить расстояние между параллельными прямой и плоскостью, между двумя параллельными плоскостями.

Библиографический список

1. Гордон В.О., Семенцов-Огиевский М.А. Курс начертательной геометрии. – М.: Наука, 2000 – 272с.

2. Крылов Н.Н. Начертательная геометрия. – М.: Высшая школа, 2007 – 224с.

3. Локтев О.В. Краткий курс начертательной геометрии. – М.: Высшая школа, 2001 – 130с.

4. Фролов С.А. Начертательная геометрия. М.: Машиностроение, 1983 – 240с.