Ход решения. 1. На эпюре проекции перпендикуляра к прямой можно построить, если прямая параллельна плоскости проекций

1. На эпюре проекции перпендикуляра к прямой можно построить, если прямая параллельна плоскости проекций. Поэтому сначала строим дополнительную ортогональную проекцию прямой и точки А на плоскости π₄, параллельной прямой l и перпендикулярной к π₁. При этом ось х₁₄ параллельна l_1. Для построения дополнительной проекции прямой l на ней отмечены точки 1 и 2 (рис. 50).

2. Проводим дополнительную проекцию А₄K₄ перпендикуляра (А₄K₄ 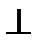l₄), а затем строим горизонтальную проекцию А₁К₁. Построена также и фронтальная А₂К₂ проекция перпендикуляра АК.

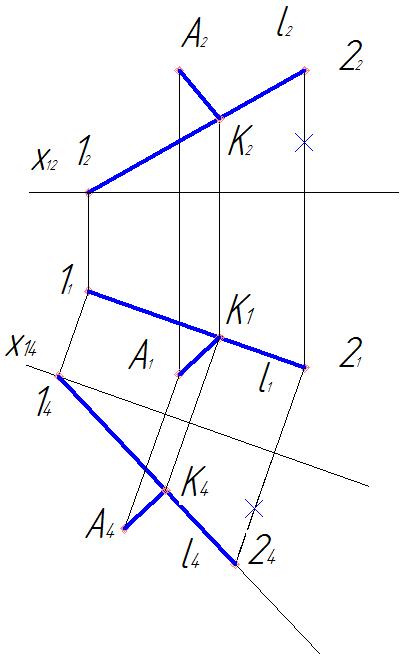
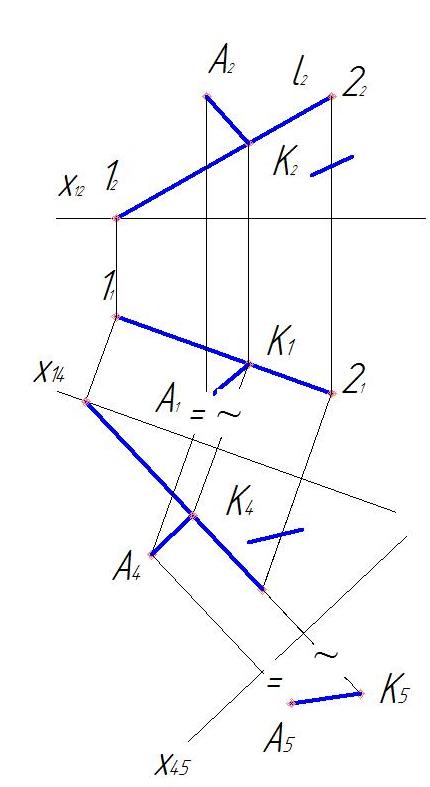
Рис. 50 Рис. 51

3. По двум данным проекциям отрезка АК (А₁К₁ и А₄K₄) находим его длину, построив дополнительную ортогональную проекцию отрезка на плоскости π₅, параллельной АК и перпендикулярной к π₄ (рис. 51).

Аналогично можно определить расстояние между двумя параллельными прямыми.

Задача 12.Определить расстояние от точки А до плоскости α(ΔВСD) (рис.52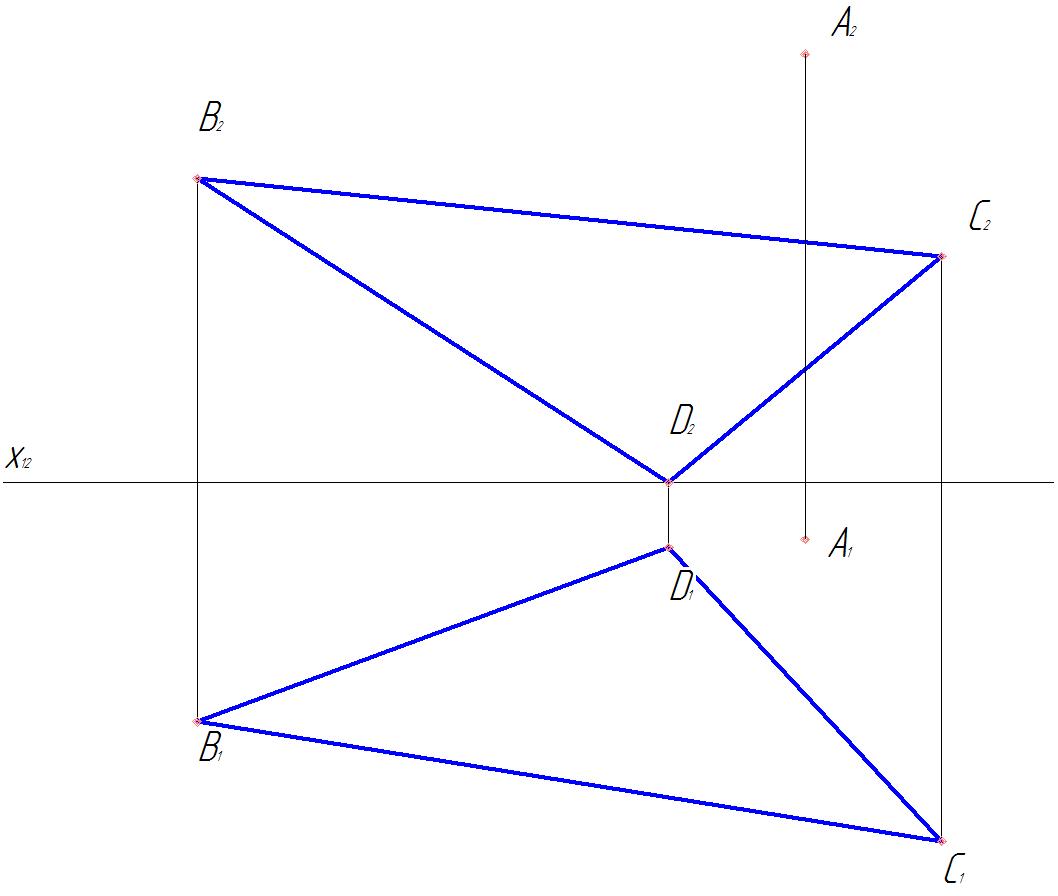

Рис. 52

Расстоянием от точки до плоскости является длина отрезка перпендикуляра, опущенного из точки на плоскость.

Если плоскость является проецирующей, то перпендикуляр к ней параллелен плоскости проекций и длина проекции его отрезка на этой плоскости проекций равна искомому расстоянию. Исходя из этого построим дополнительную ортогональную проекцию плоскости α и точки А на плоскости π₄, перпендикулярной к плоскости α и к плоскости π₁.