Ход решения. 1. Заключаем прямую l в плоскость частного положения так, чтобы при пересечении конуса с плоскостью была простая линия пересечения – окружность

1. Заключаем прямую l 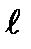в плоскость частного положения так, чтобы при пересечении конуса с плоскостью была простая линия пересечения – окружность. В данной задаче α – горизонтальная плоскость, l₂ 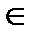α₂.

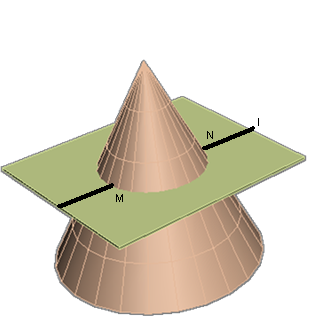(рис. 29).

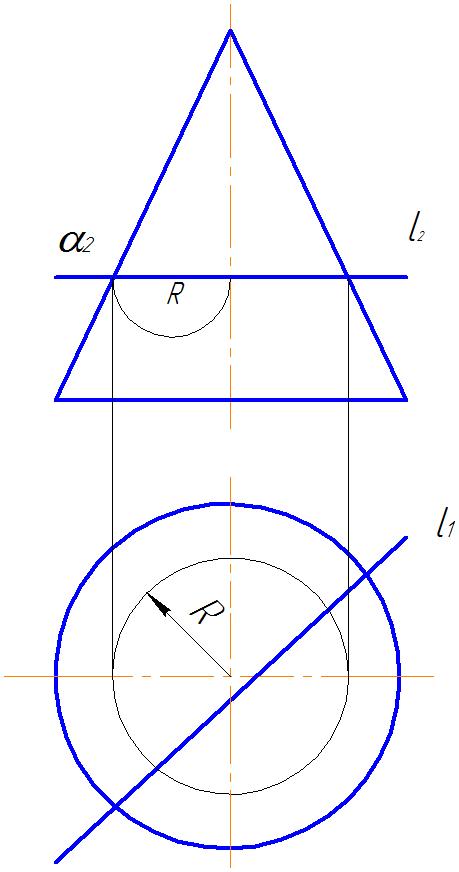
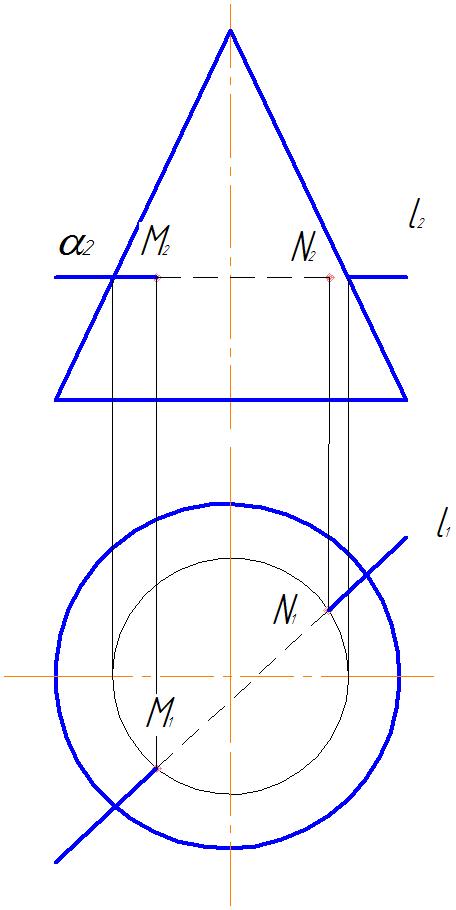
Рис. 29 Рис.30

2. Строим линию пересечения конуса с плоскостью α. Это окружность радиуса R.

3. На пересечении горизонтальной проекции l₁ и окружности радиуса R отметим искомые горизонтальные проекции M ₁ и N ₁. M ₂ и N₂ отмечаем на l₂ .

4. Определяем видимость прямой l. Между получившимися точками M и N прямая всегда невидима. Горизонтальная проекция прямая l₁ видима (невидима только от M₁ до N₁). Фронтальная проекция l₂ до М₂ видима, т.к. точка М лежит на видимой части конуса относительно π₂. Точка N лежит на невидимой части конуса относительно π₂, следовательно, фронтальная проекция l₂ от N₂ до очерковой образующей невидима. За очертаниями конуса прямая l всегда видима (рис.30 ).2

Пример 2. Гранная поверхность - призма (рис.31 )

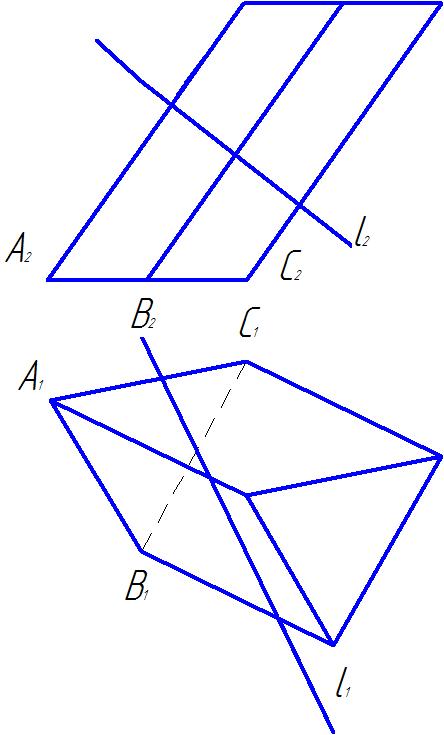
Рис. 31