Ход решения. 1. Через прямую l проводим вспомогательную плоскость частного положения, например, горизонтально-проецирующую α π1

1. Через прямую l проводим вспомогательную плоскость частного положения, например, горизонтально-проецирующую α 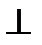π₁. l₁ 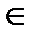α₁(рис. 16).

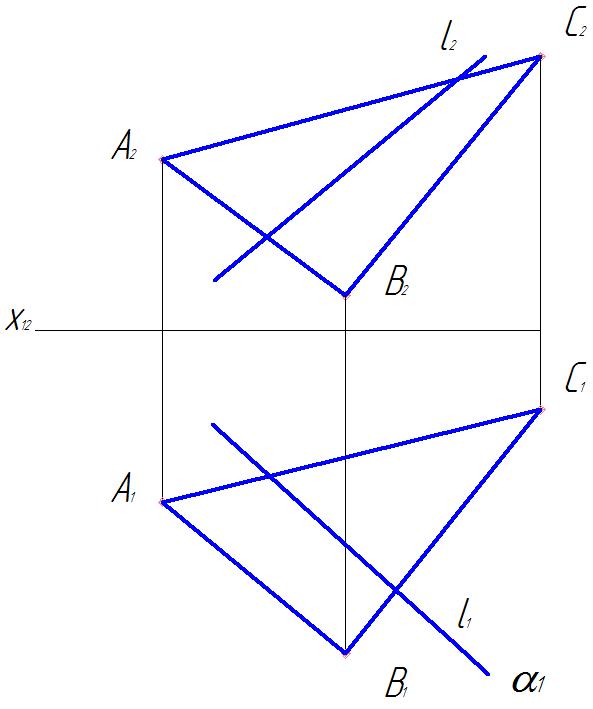
Рис. 16

2. Строим линию пересечения MN заданной и вспомогательной плоскостей. М₁=А₁С₁ ∩ α_1, М₂ 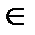А₂С₂ и N₁=В₁С₁∩α _1,N₂ 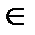В₂С₂ (рис. 17).

3. Строим точку пересечения К заданной прямой l с линией пересечения МN. К₂= М₂N₂∩l₂. К₁ находится в пересечении линии проекционной связи, проведенной из К₂ и М'N'.

4. Определяем видимость прямой относительно ΔАВС с помощью конкурирующих точек.

Определяем видимость относительно плоскости π₂ .Отметим фронтальную проекцию 1 ₂совпадающую с 2₂ Горизонтальную проекцию 2₁ отметим на А₁С₁, а 1₁ на l₁. Горизонтальная проекция 1₁ лежит перед 2₁, следовательно, фронтальная проекция 2₂не видима относительно π₂. Точка 1 лежит на прямой l, она видима на π₂, следовательно фронтальная проекция l₂ от 1₂ 2₂ до К₂ видима, в точке К₂ видимость меняется на противоположную.

Определим видимость прямой l относительно плоскость π₁. Отметим горизонтальную проекцию 3₁ совпадающую с горизонтальной проекцией М₁. М₂ 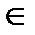А₂С₂ уже отмечена, 3₂ 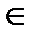l₂. Фронтальная проекция М лежит выше фронтальной проекции 3₂, следовательно, точка М видима относительно π₁. Точка 3 лежит на l, следовательно от М₁ ≡3 ₁ до К ₁, горизонтальная проекция l ₁ невидима. В горизонтальной проекции К ₁ видимость меняется на противоположную. За границами ΔАВС прямая l везде видима.

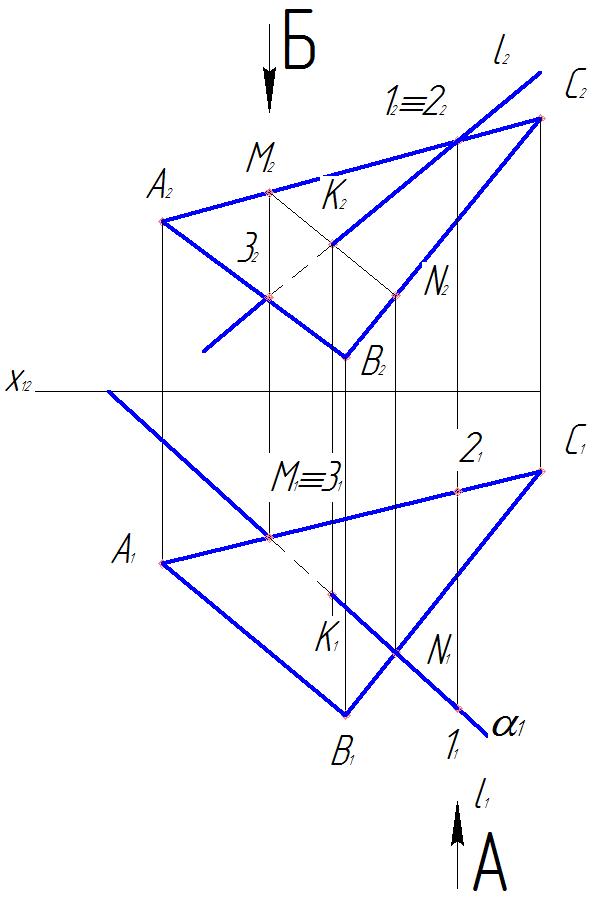
Рис. 17

Задача 6.Построить линию пересечения плоскости общего положения с заданной поверхностью.

Пример1.Трехгранная призма (рис.18).

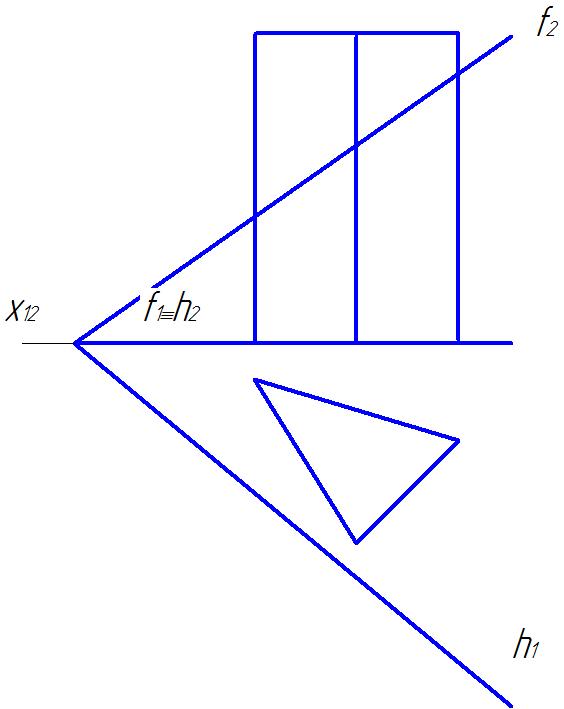
Рис.18