Ход решения. 1. Отметим общие горизонтальные проекции Q1 и T1 на пересечении горизонтальных проекций треугольников АВС и MNK (рис.9).

1. Отметим общие горизонтальные проекции Q₁ и T₁ на пересечении горизонтальных проекций треугольников АВС и MNK (рис.9).

2. Фронтальные проекции Q₂ и T₂ ищем на линиях проекционной связи в ΔM₂N₂K₂.

3. Линия пересечения QT определена QT (Q ₂T₂ и Q₁T₁).

4. Определим видимость плоских фигур, т.к. плоскости считаются непрозрачными. Видимость горизонтальной проекции фигур определять не надо, т.к. ΔАВС проецируется в прямую линию, проекция M₁N₁K₁видима. Определим видимость плоских фигур относительно плоскости проекций π₂. Для этого рассмотрим конкурирующие точки 1 и 2, лежащие на скрещивающихся прямых ВС и МK. Фронтальные проекции 1₂ и 2₂ совпадают, а горизонтальная проекция 2₁ находится перед горизонтальной проекцией 1₁. Точка 1₂ не видима относительно плоскости проекций π₂. Далее рассуждаем так: точка 2 лежит на ΔАВС, следовательно, фронтальная проекция ΔА₂В₂С₂ видима на π₂ с той стороны, где находятся точки 1₂ и 2₂. После фронтальной проекции линии пересечения Q₂ и T₂ видимость Δ А₂В₂С₂ меняется на противоположную, т.е. он становится невидимым (рис.9).

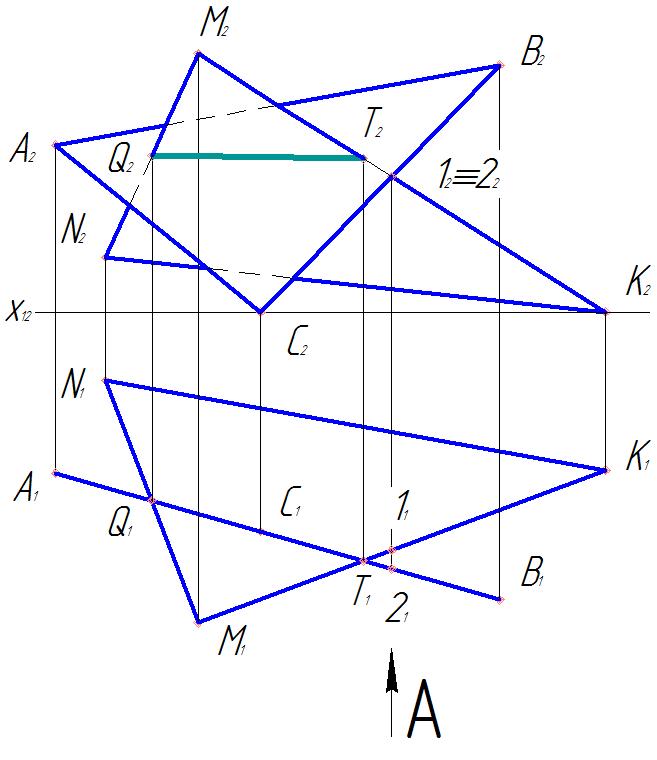
Рис. 9

Задача 4.Построить линию пересечения плоскостей.(рис.10)

Заданы две плоскости общего положения.

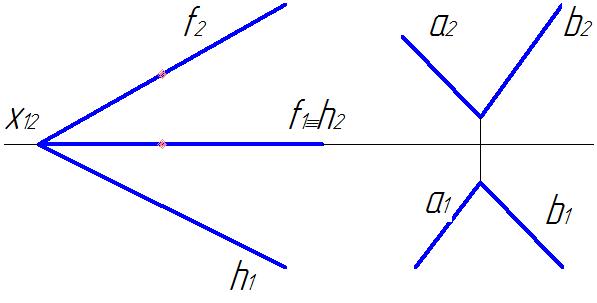
Рис. 10