Ход решения. Ребра призмы перпендикуляры горизонтальной плоскости проекций, поэтому горизонтальные проекции A1,В1,С1 точек встречи ребер призмы с плоскостью совпадают с

Ребра призмы перпендикуляры горизонтальной плоскости проекций, поэтому горизонтальные проекции A₁,В_1,С₁ точек встречи ребер призмы с плоскостью совпадают с горизонтальными проекциями вершин основания призмы. Фронтальные проекции А₂,В₂,С₂ точек А, В, С будут лежать на фронтальных проекциях фронталей плоскости, проведенных через эти точки (рис.19).

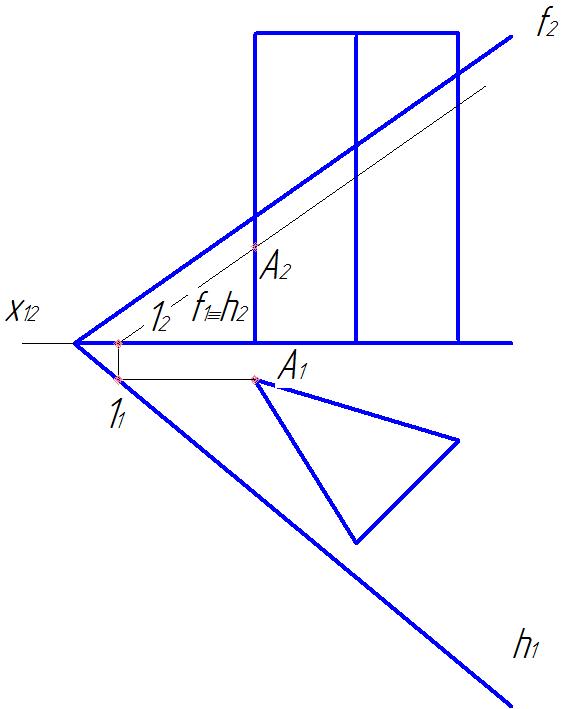
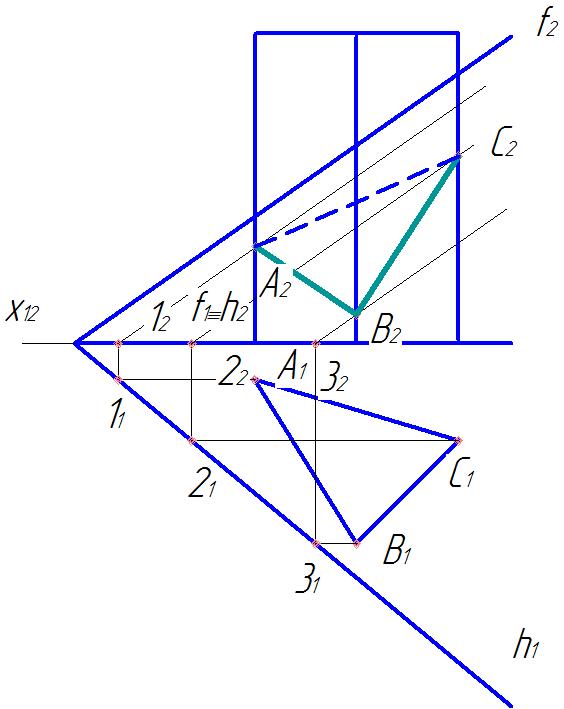
Рис. 19 Рис.20

Полученные точки соединили с учетом видимости граней призмы (рис.20).

Пример 2. Пересечение цилиндрической поверхности плоскостью общего положения (рис.21).

Рис.21

Прямая круговая цилиндрическая поверхность пересекается плоскостью общего положения. Плоскость задана пересекающимися прямыми m и n. Построить проекции линии пересечения.

Линией пересечения прямой круговой цилиндрической поверхности плоскостью общего положения является эллипс.

Данная цилиндрическая поверхность является горизонтально-проецирующей, так как ее образующие перпендикулярны горизонтальной плоскости проекций. Следовательно, линия пересечения, как принадлежащая такой поверхности, на горизонтальную плоскость проекций проецируется в виде очерка этой поверхности, т.е. в виде окружности. На фронтальную плоскость проекций линия пересечения проецируется в виде эллипса.

Отметим опорные (базовые), обязательные для построения точки, принадлежащие линии пересечения:

- точки, наиболее и наименее удаленные от плоскостей проекций;

- точки перехода от видимой к невидимой части линии пересечения

- Ход решения:

1.В рассматриваемом примере фигурой сечения является эллипс, имеющий большую и малую ось..

Большая ось принадлежит линии наибольшего ската секущей плоскости, проходящей через ось вращения цилиндрической поверхности и располагающейся перпендикулярно горизонталям секущей плоскости. Для построения большой оси необходимо на горизонтальной проекции через центр основания провести прямую перпендикулярную прямой m, являющейся горизонталью секущей плоскости. Отметить точки М и N пересечения с очерком цилиндрической поверхности, и точку 1 с прямой m. Спроецируем точку 1 на фронтальную проекцию прямой m. Отрезок MN – большая ось эллипса (рис.22)

Малая ось эллипса перпендикулярна большой оси. Взаимная перпендикулярность между осями сохранится только на горизонтальной проекции, так как малая ось, являясь горизонталью секущей плоскости, параллельна горизонтальной плоскости проекций, а большая ось, являясь прямой общего положения. Следовательно, для построения малой оси нужно на горизонтальной проекции через центр эллипса провести прямую перпендикулярно отрезку MN и отметить точки А и В пересечения с очерком цилиндрической поверхности.

Центр эллипса (точка О) на горизонтальной проекции совпадает с центром основания цилиндрической поверхности. Фронтальная проекция точки О является точкой пересечения фронтальных проекций большой и малой оси.

.Наиболее и наименее удаленные от горизонтальной плоскости проекций точки фигуры сечения определяются на фронтальной проекции. Это точки М и N, принадлежащие большой оси эллипса.

2.Наиболее и наименее удаленные от фронтальной плоскости проекций точки определяются на горизонтальной проекции. Это точки E и F – точки пересечения вертикальной оси симметрии с очерком цилиндрической поверхности. Для построения их фронтальной проекции следует использовать горизонтали секущей плоскости(рис.23).

.3. Точками перехода от видимой к невидимой части линии пересечения являются точки, принадлежащие очерковым образующим. На горизонтальной проекции им соответствуют точки пересечения очерка цилиндрической поверхности с горизонтальной осью симметрии – точки C и D. Их перенос на фронтальную проекцию выполняется также с помощью горизонталей секущей плоскости (рис.24).

Для более точного построения проекций линии пересечения следует ввести дополнительные точки. Целесообразно брать точки, принадлежащие тем же горизонталям, которые были использованы для построения опорных точек.

Соединяем с учетом видимости с помощью лекала полученные точки.

Рис.22 Рис .23 Рис.24

Задача 7.Построить линию пересечения поверхности конуса с плоскостью (рис. 25).

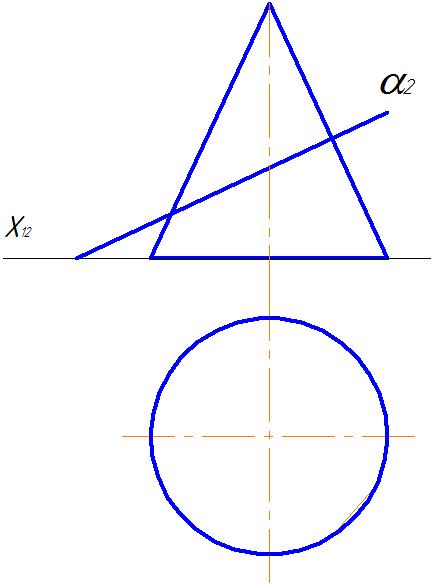
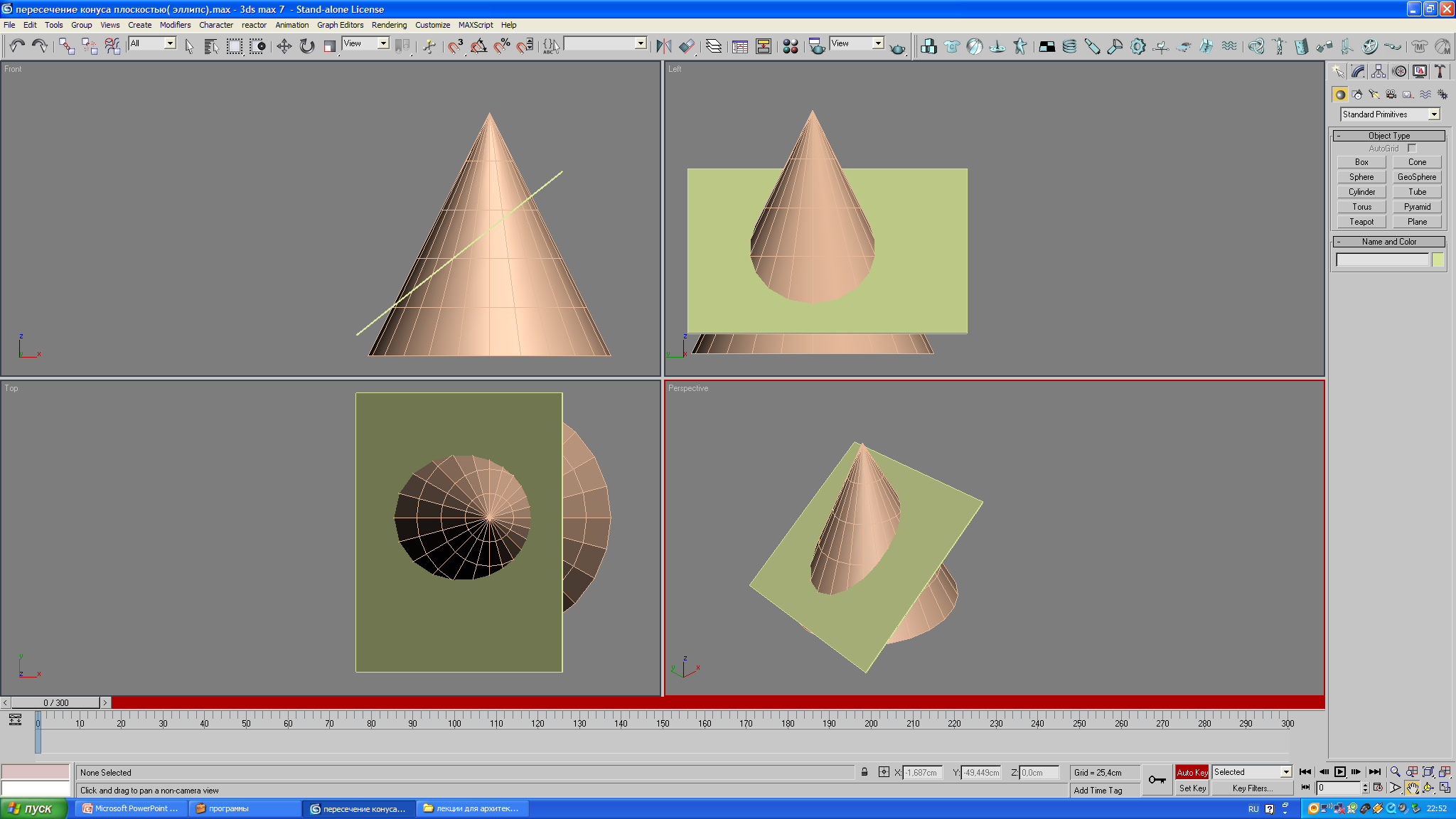
Рис. 25

Задан конус и плоскость частного положения, в данной задаче плоскость фронтально-проецирующая α 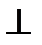π₂. Линия пересечения поверхности конуса с фронтально-проецирующей плоскостью представляет собой эллипс. Эллипс – это лекальная кривая, которая строится минимум по 8 точкам. Фронтальная проекция эллипса совпадает с фронтальной проекцией плоскости α.