Ранг матрицы.
Рассмотрим матрицу А размера 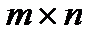

Выделим в ней k строк и k столбцов ( 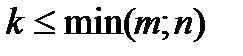 ). Из элементов, стоящих на пересечении выделенных строк и столбцов, составим определитель k-гo порядка. Все такие определители называются минорами этой матрицы. Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Обозначается r,r(A) или rang A.
). Из элементов, стоящих на пересечении выделенных строк и столбцов, составим определитель k-гo порядка. Все такие определители называются минорами этой матрицы. Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Обозначается r,r(A) или rang A.
Минор, порядок которого определяет ранг матрицы, называется базисным.У матрицы может быть несколько базисных миноров.
Пример.Найти ранг матрицы:
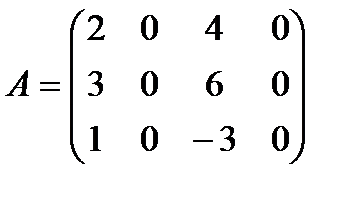
Решение: Все миноры 3-го порядка равны нулю. Есть минор 2-го порядка 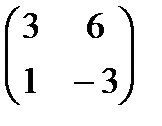 , отличный от нуля
, отличный от нуля 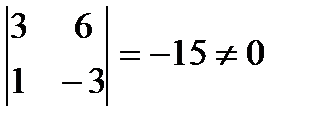 . Значит, r(А) = 2. Базисный минор
. Значит, r(А) = 2. Базисный минор 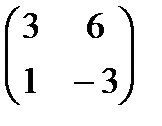 . Минор
. Минор 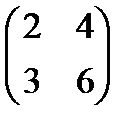 не является базисным, т.к.
не является базисным, т.к. 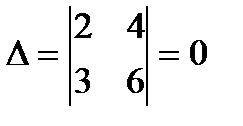
Содержание работы
Задание 1. Дана матрица А
1.1 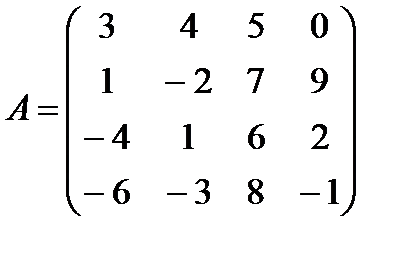 1.2.
1.2. 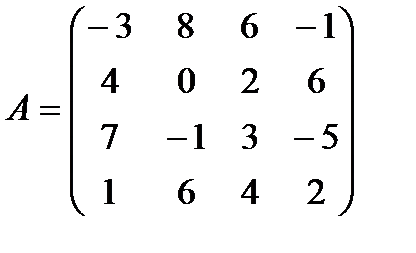 1.3
1.3 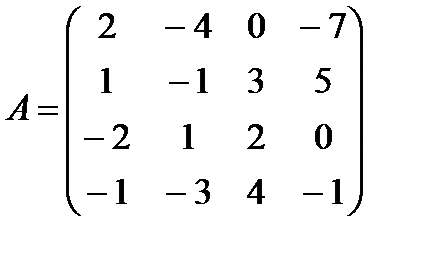
1.4 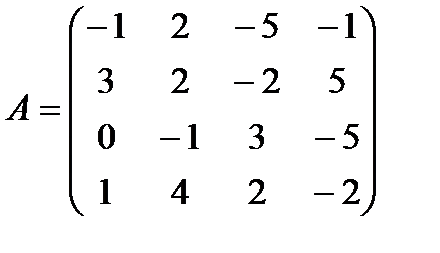 1.5
1.5 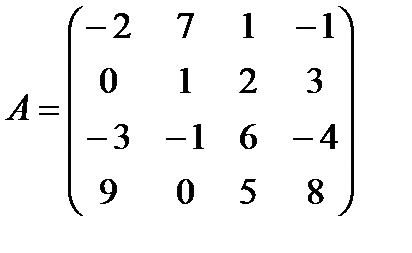
1). Назовите размер матрицы.
2). Назовите все элементы матрицы.
3). Назовите все элементы матрицы образующие главную диагональ.
4). Составьте диагональную матрицу Ад.
5). Составьте треугольную матрицу Ат из матрицы А.
6). Выпишите 2-й вектор-столбец матрицы А.
7). Выпишите 3-ю вектор-строку матрицы А.
8). Составьте транспонированную матрицу Ат матрице А.
Задание 2. Даны матрицы А и В
2.1. 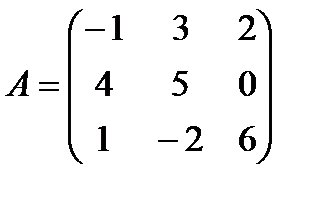 и
и 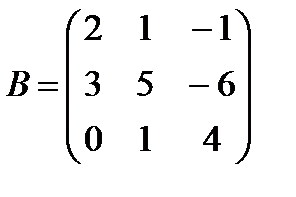 2.2.
2.2. 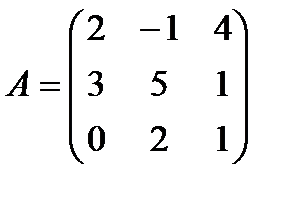 и
и 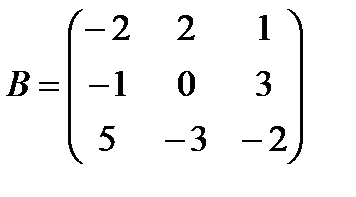
2.3 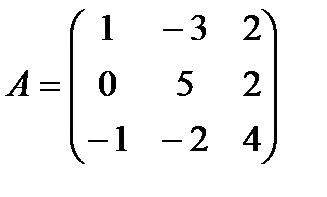 и
и 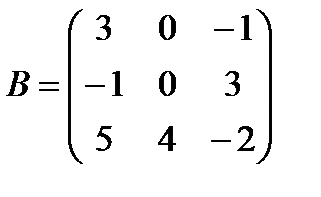 2.4
2.4 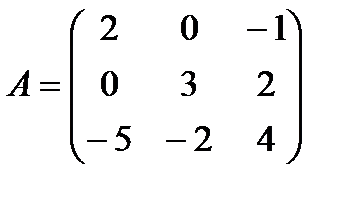 и
и 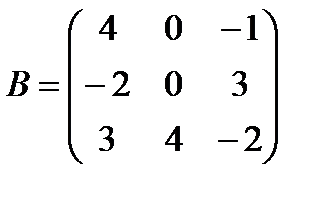
2.5. 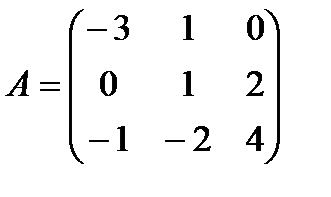 и
и 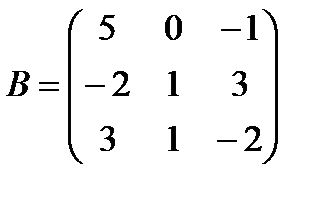
Вычислите:
1. А+В
2. А – В
3. 3А
4. – В
5. А·В
Задание 3. Вычислите определители:
3.1 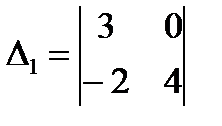 ;
; 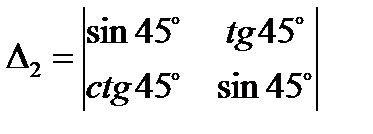 ;
; 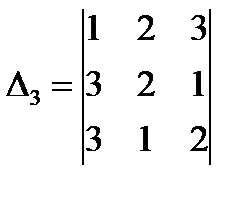 ;
; 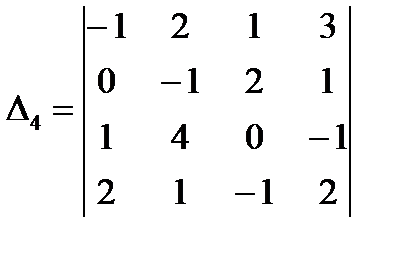
3.2 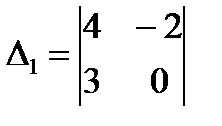 ;
; 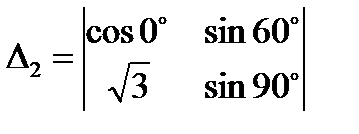 ;
; 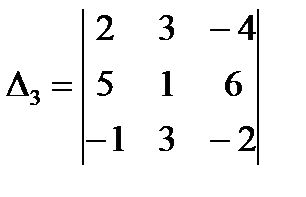 ;
; 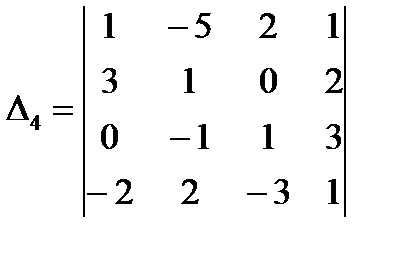
3.3. 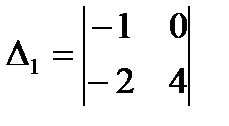 ;
; 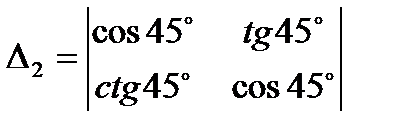 ;
; 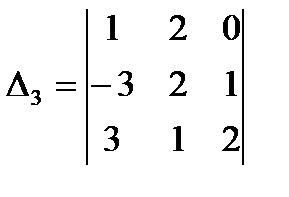 ;
; 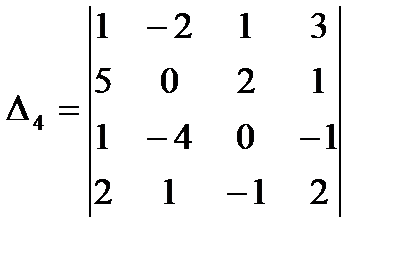
3.4 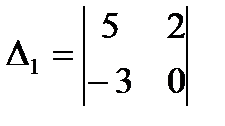 ;
; 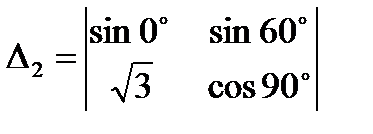 ;
; 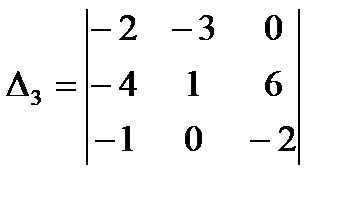 ;
; 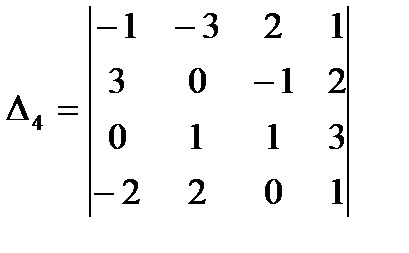
3.5 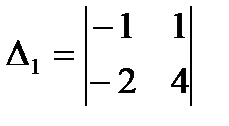 ;
; 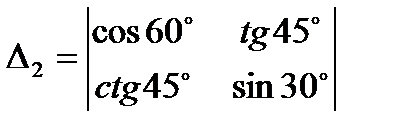 ;
; 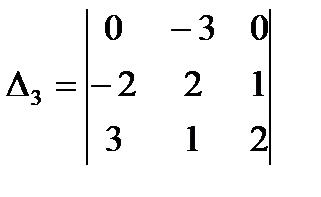 ;
; 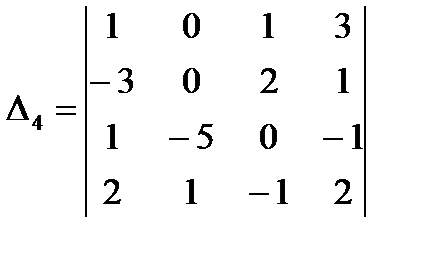
Задание 4. Для матрицы А найдите обратную матрицу А-1 и убедитесь, что 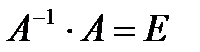
4.1. 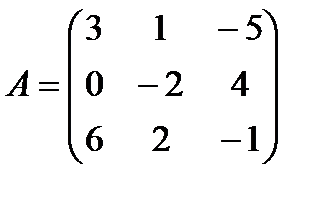 4.2.
4.2. 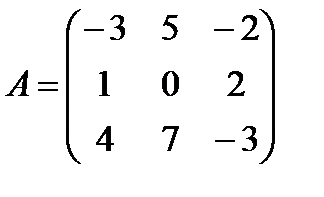 4.3.
4.3. 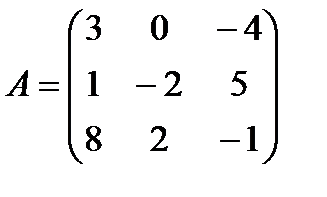
4.4. 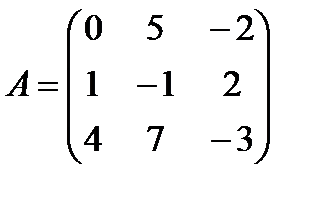 4.5.
4.5. 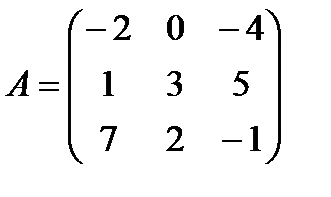
Задание 5 . Для матрицы А найдите союзную матрицу А*-
5.1. 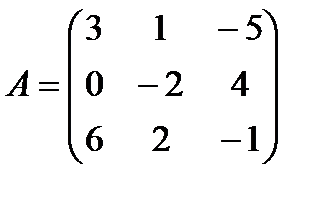 5.2.
5.2. 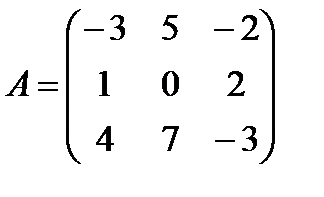 5.3.
5.3. 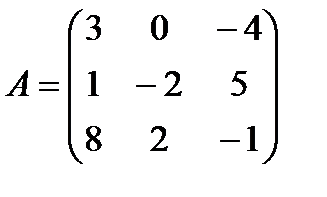
5.4. 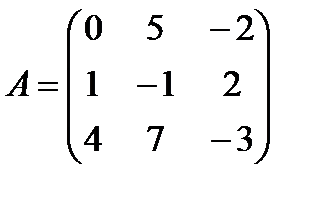 5.5.
5.5. 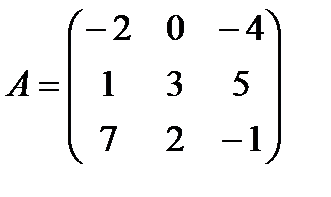
Вопросы для самоконтроля
Дана матрица 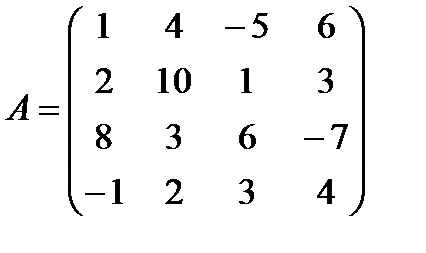
1. Назовите размер матрицы.
2. Назовите все элементы матрицы.
3. Назовите все элементы матрицы образующие главную диагональ.
4. Составьте диагональную матрицу Ад.
5. Составьте треугольную матрицу Ат из матрицы А.
6. Выпишите 3-й вектор-столбец матрицы А.
7. Выпишите 2-ю вектор-строку матрицы А.
8. Составьте транспонированную матрицу Ат матрице А.
Вычислите самостоятельно:
9. 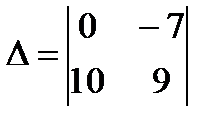 Ответ: 70
Ответ: 70
10. 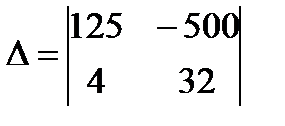 Ответ: 6000(воспользуйтесь свойством №4)
Ответ: 6000(воспользуйтесь свойством №4)
11. Решите уравнение 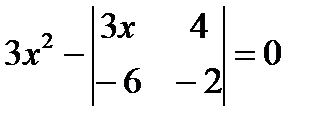 Ответ: 2 и -4
Ответ: 2 и -4
12. 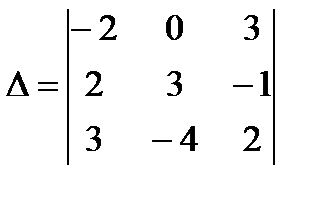 Ответ: -55
Ответ: -55
13. 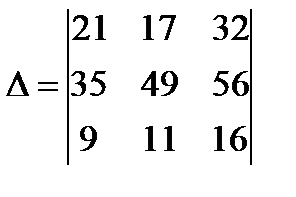 Ответ: 784(воспользуйтесь свойством №4)
Ответ: 784(воспользуйтесь свойством №4)
14. Найдите 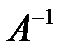 , если
, если 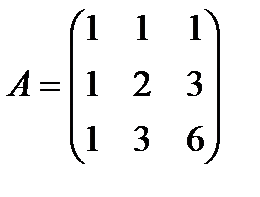
15. Что называется рангом матрицы и минором матрицы.
16. Найдите ранг матрицы 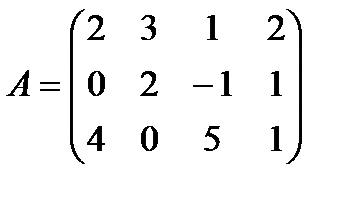
Дата добавления: 2014-12-05; просмотров: 1263;
