Произведение матриц.

Операция умножения двух матриц вводится только для случая, когда

число столбцов первой матрицы равно числу строк второй матрицы.

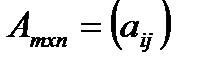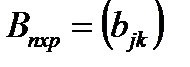Произведением матрицы и называется матрица 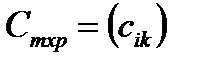такая, что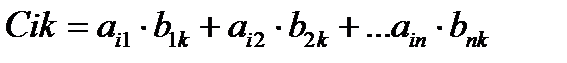

т. е. элемент i-й строки и k-го столбца матрицы произведения С равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы k-го столбца матрицы В.

Получение элемента 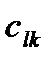схематично изображается так:

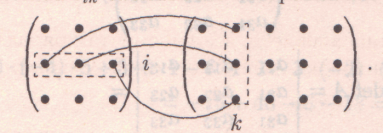
Если матрицы А и В квадратные одного размера, то произведения АВ и BА всегда существуют.

Пример. 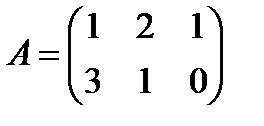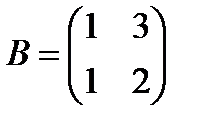, то 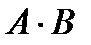не определено, 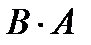определено

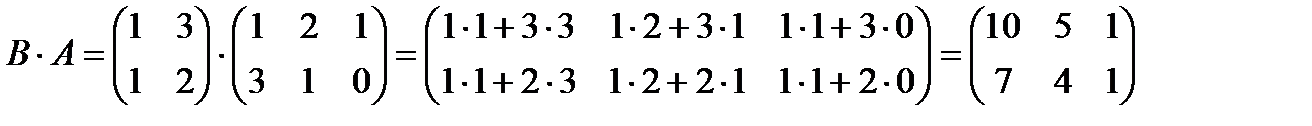
Матрицы А и В называются перестановочными, если АВ = ВА.