Решение. Точками разрыва функции являются точки разрыва функций в промежутках , , ,

Точками разрыва функции 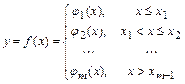являются точки разрыва функций 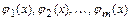в промежутках , ,…, , 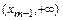кроме того, точками возможного разрыва функции 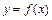являются точки 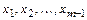в окрестности которых и в самих точках функция задаётся разными аналитическими выражениями.

Точка 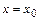является точкой непрерывности функции 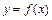тогда и только тогда, когда: .

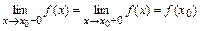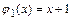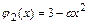а)Поскольку функции и непрерывны в промежутках 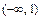и 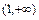как элементарные функции, определённые в каждой точке данных промежутков, то непрерывностьфункции 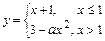может нарушиться только в точке её возможного разрыва .

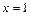Определяем значение параметра 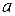из условия непрерывности функции 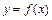в точке 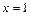: 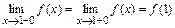. Вычисляя 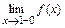, , 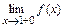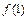: 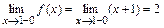, , 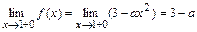, 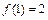из условия непрерывности 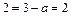, находим .

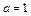График непрерывной функции 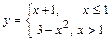имеет вид изображённый на рис. 1.

б)Функци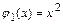и и 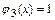непрерывны в промежутках 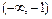и 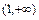как элементарные функции, определённые в каждой точке данных промежутков, а функция 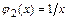в промежутке 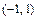имеет точкой разрыва точку 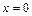, в которой она не определена. Тогда для функции 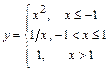точка 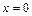является точкой разрыва, а точк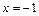и и 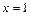, в окрестности которых и в самих точках функция задаётся разными аналитическими выражениями, являются точками возможного разрыва.

Исследуем на непрерывность точки :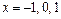

1)

.

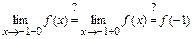
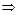
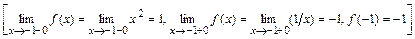
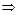
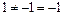Следовательно, точка 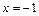- точка разрыва 1-го рода функции .

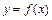2)

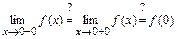
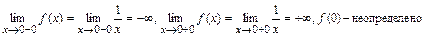Следовательно, точка 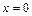- точка бесконечного разрыва (2-го рода) функции .

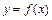3)

.

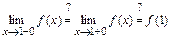
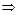
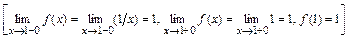
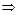
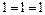Следовательно, точка 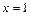- точка непрерывности функции .

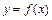График функции 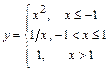имеет вид, изображённый на рис.2.

Ответ: а)Функция 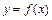непрерывна при 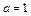(рис.1); б) 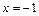- точка разрыва 1-го рода, 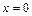-точка бесконечного разрыва функции 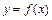(рис.2).

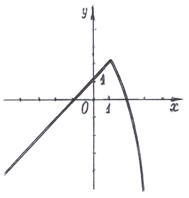
Рис.1 Рис.2

12.1-30.Даны комплексные числа 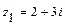, , 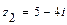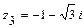и алгебраическое уравнение 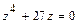. Требуется: а)вычислить 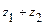, , 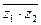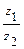; б)представить комплексное число 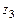в тригонометрической форме, вычислить 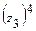и результат представить в алгебраической форме; в)найти все корни алгебраического уравнения на множестве комплексных чисел.