Г) ; д) ; е) .
8.1–30.Установить, какую кривую определяет алгебраическое уравнение второго порядка, построить её:
а) 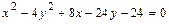 ;б)
;б) 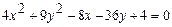 ;
;
в) 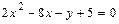 .
.
Решение:
а)Выделяя полные квадраты в левой части уравнения 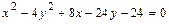 ,преобразуем его следующим образом:
,преобразуем его следующим образом:

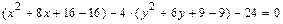
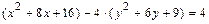
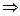

.
Полученное уравнение определяет гиперболу с центром в точке 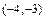 и осями симметрии параллельными координатным осям. Для построения гиперболы в системе координат
и осями симметрии параллельными координатным осям. Для построения гиперболы в системе координат  : 1) отмечаем центр гиперболы
: 1) отмечаем центр гиперболы 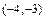 ; 2) проводим через центр
; 2) проводим через центр 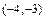 пунктиром оси симметрии гиперболы; 3) строим пунктиром основной прямоугольник гиперболы с центром
пунктиром оси симметрии гиперболы; 3) строим пунктиром основной прямоугольник гиперболы с центром 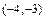 и сторонами
и сторонами 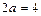 и
и  параллельными осям симметрии; 4)проводим через противоположные вершины основного прямоугольника пунктиром прямые, являющиеся асимптотами гиперболы, к которым неограниченно близко при бесконечном удалении от начала координат приближаются ветви гиперболы, не пересекая их; 5) изображаем сплошной линией ветви гиперболы (рис. 1).
параллельными осям симметрии; 4)проводим через противоположные вершины основного прямоугольника пунктиром прямые, являющиеся асимптотами гиперболы, к которым неограниченно близко при бесконечном удалении от начала координат приближаются ветви гиперболы, не пересекая их; 5) изображаем сплошной линией ветви гиперболы (рис. 1).
Ответ:Гипербола с центром в точке 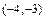 (см. рис.1)..
(см. рис.1)..
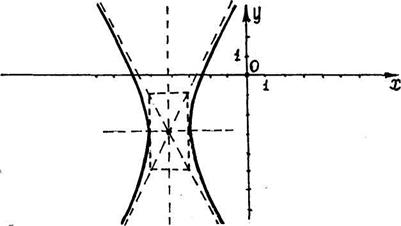
Рис.1
б)Выделяя полные квадраты в левой части
уравнения 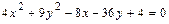 ,преобразуем его следующим образом:
,преобразуем его следующим образом: 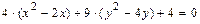

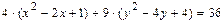
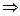
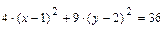
.
Полученное уравнение определяет эллипс с центром в точке  и осями симметрии параллельными осям координат. Для построения эллипса в системе координат
и осями симметрии параллельными осям координат. Для построения эллипса в системе координат  : 1) отмечаем центр эллипса
: 1) отмечаем центр эллипса  ; 2) проводим через центр
; 2) проводим через центр  пунктиром оси симметрии эллипса; 3) строим пунктиром основной прямоугольник эллипса с центром
пунктиром оси симметрии эллипса; 3) строим пунктиром основной прямоугольник эллипса с центром  и сторонами
и сторонами 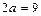 и
и  параллельными осям симметрии; 4) изображаем сплошной линией эллипс, вписывая его в основной прямоугольник так, чтобы эллипс касался его сторон в точках пересечения прямоугольника с осями симметрии (рис.2).
параллельными осям симметрии; 4) изображаем сплошной линией эллипс, вписывая его в основной прямоугольник так, чтобы эллипс касался его сторон в точках пересечения прямоугольника с осями симметрии (рис.2).
Ответ:Эллипс с центром в точке  (см. рис.2).
(см. рис.2).
в). Выделяя полные квадраты в левой части уравнения 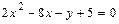 ,преобразуем его следующим образом:
,преобразуем его следующим образом:
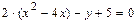
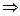
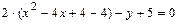
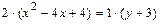
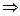
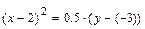
Полученное уравнение определяет параболу с вершиной в точке 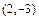 и осью симметрии параллельной оси
и осью симметрии параллельной оси 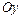 . Для построения параболы в системе координат
. Для построения параболы в системе координат  : 1) отмечаем вершину параболы
: 1) отмечаем вершину параболы 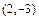 ; 2) проводим через вершину
; 2) проводим через вершину 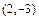 пунктиром ось симметрии параболы; 3) изображаем сплошной линией параболу, направляя её ветвь, с учётом того, что параметр параболы
пунктиром ось симметрии параболы; 3) изображаем сплошной линией параболу, направляя её ветвь, с учётом того, что параметр параболы  , в положительную сторону оси
, в положительную сторону оси 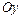 (рис.3).
(рис.3).
Ответ:Парабола с вершиной в точке 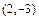 (см. рис.3).
(см. рис.3).
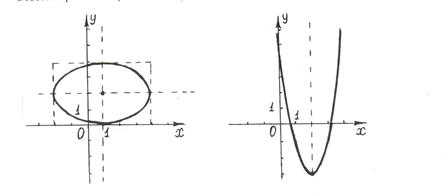
Рис.2. Рис.3.
9.1-30.Требуется:
а)найтиобласть определения функции  ;
;
б)установить чётность (нечётность) функции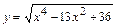 .
.
Решение. а)Естественную область определения находим как множество 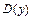 всех значений аргумента
всех значений аргумента 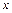 функции, для которых формула
функции, для которых формула  имеет смысл:
имеет смысл:  . Решив (на числовой прямой) систему неравенств
. Решив (на числовой прямой) систему неравенств 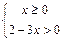 , устанавливаем, что геометрическим образом множества
, устанавливаем, что геометрическим образом множества 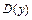 является промежуток
является промежуток  .
.
б)Находимсначала естественнуюобласть определения функции 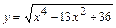 :
: 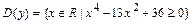 . Решив (на числовой прямой) неравенство
. Решив (на числовой прямой) неравенство  , устанавливаем, что геометрическим образом множества
, устанавливаем, что геометрическим образом множества 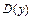 является объединение промежутков
является объединение промежутков 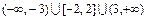 .
.
Так как область 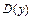 является симметричной относительно точки
является симметричной относительно точки 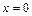 , то проверяем выполнение для всех
, то проверяем выполнение для всех 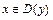 условий:
условий: 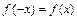 или
или 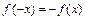 , учитывая чётность и нечётность основных элементарных функций, входящих в аналитическое выражение
, учитывая чётность и нечётность основных элементарных функций, входящих в аналитическое выражение  .
.
Если область 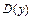 не симметрична относительно точки
не симметрична относительно точки 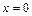 , то
, то  на этом множестве является функцией общего вида.
на этом множестве является функцией общего вида.
Для этого находим 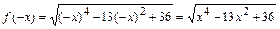 . Поскольку
. Поскольку 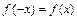 для всех
для всех 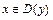
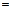
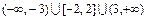 , то функция
, то функция 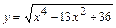 является чётной.
является чётной.
Ответ: а) 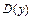
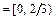 ,
,  ;
;
б)функция 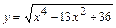 - чётная.
- чётная.
10.1-30.Вычислить пределы (не пользуясь правилом Лопиталя):
а) 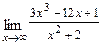 б)
б) 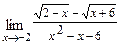 в)
в)  г)
г) 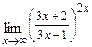 д)
д) 
Вычисление предела 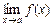 , где
, где 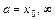 , начинают всегда с подстановки в
, начинают всегда с подстановки в  предельного значения её аргумента
предельного значения её аргумента 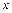 . В результате могут получиться неопределённости
. В результате могут получиться неопределённости 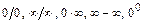 ,
, 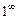 ,
, 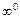 , которые раскрывают тождественными преобразованиями
, которые раскрывают тождественными преобразованиями  такими, чтобы преобразованное выражение получилось определённым. При вычислении пределов используют свойства конечных пределов и бесконечно больших функций, а также следующие известные пределы:
такими, чтобы преобразованное выражение получилось определённым. При вычислении пределов используют свойства конечных пределов и бесконечно больших функций, а также следующие известные пределы: 
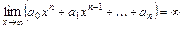 ,
, 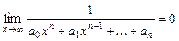 ,
,  (
(  ),
), 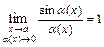 ,
, 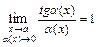 ,
, 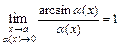 ,
,  ,
, 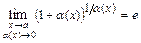 .
.
Решение. а) 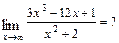 При подстановке вместо переменной
При подстановке вместо переменной 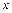 её предельного значения
её предельного значения 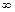 получим неопределённость
получим неопределённость 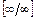 . Для её раскрытия сначала разделим числитель и знаменатель дроби на
. Для её раскрытия сначала разделим числитель и знаменатель дроби на 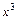 (старшую степень переменной
(старшую степень переменной 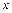 в числителе и знаменателе), после чего используем свойства конечных пределов и бесконечно больших функций. Получим
в числителе и знаменателе), после чего используем свойства конечных пределов и бесконечно больших функций. Получим 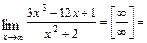

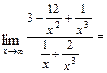
.
б) 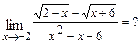 При подстановке вместо переменной
При подстановке вместо переменной 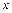 её предельного значения
её предельного значения  получим неопределённость
получим неопределённость 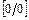 . Для её раскрытия выделим в числителе и знаменателе дроби общий множитель вида
. Для её раскрытия выделим в числителе и знаменателе дроби общий множитель вида 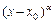 , где
, где 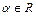 - некоторое число, т.е. множитель
- некоторое число, т.е. множитель 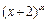 . Затем сократим на него числитель и знаменатель дроби, после чего используем свойства пределов.
. Затем сократим на него числитель и знаменатель дроби, после чего используем свойства пределов.
1) В квадратном трёхчлене 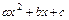 множитель выделяют разложением квадратного трёхчлена по формуле
множитель выделяют разложением квадратного трёхчлена по формуле 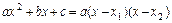 , где
, где 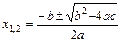 . 2) В выражении
. 2) В выражении 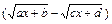 множитель выделяют следующим способом:
множитель выделяют следующим способом: 
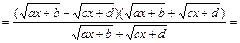
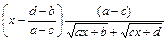 .
.
В результате получим 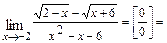
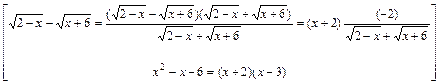
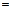
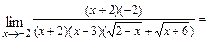
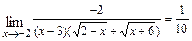 .
.
в) 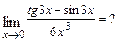 При подстановке вместо переменной
При подстановке вместо переменной 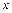 её предельного значения
её предельного значения 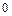 получим неопределённость
получим неопределённость 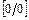 . Выделим в числителе множители вида
. Выделим в числителе множители вида 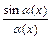 , где
, где 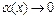 при
при 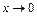 и используем свойства пределов. Получим
и используем свойства пределов. Получим
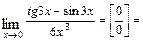

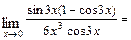
Для раскрытия неопределённостей 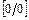 , содержащих тригонометрические и обратные тригонометрические функции, в числителе и знаменателе дроби выделяют сначала множители вида:
, содержащих тригонометрические и обратные тригонометрические функции, в числителе и знаменателе дроби выделяют сначала множители вида: 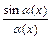 ,
,  ,
, 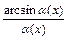 ,
, 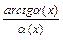 , где
, где 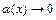 при
при 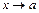 , используя формулы тригонометрии:
, используя формулы тригонометрии: 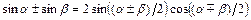 ,
, 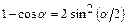 ,
, 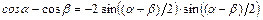 . После чего применяют свойства пределов, учитывая, что:
. После чего применяют свойства пределов, учитывая, что: 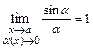 ,
, 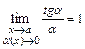 ,
, 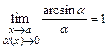 ,
, 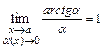 .
.
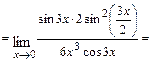
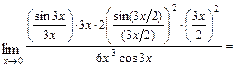
.
г) 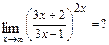
Для раскрытия неопределённости 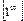 , возникающей при вычислении предела
, возникающей при вычислении предела 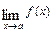 , где
, где 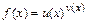 ,
, 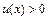 , сначала выражение
, сначала выражение  представляют в виде
представляют в виде  , где
, где 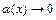 при
при 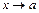 . После чего используют свойства пределов, заменяя выражение
. После чего используют свойства пределов, заменяя выражение 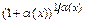 его предельным значением
его предельным значением 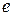 и учитывая, что
и учитывая, что 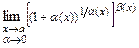 =
= 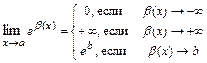 .
.
При подстановке вместо переменной 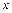 её предельного значения
её предельного значения 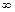 получим неопределённость
получим неопределённость 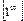 . Представим
. Представим 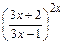 в виде
в виде 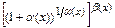 , где
, где 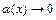 при
при 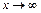 ,следующим способом:
,следующим способом: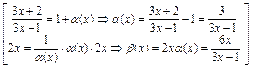
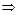
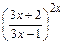 =
= 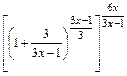 . Тогда учитывая, что
. Тогда учитывая, что 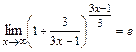 ,
, 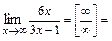
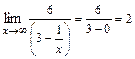 , получим
, получим 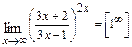 =
= 
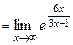 =
= 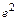 .
.
Дата добавления: 2014-12-04; просмотров: 986;
