Решение. 1в)Записываем расширенную матрицу системы:

1в)Записываем расширенную матрицу системы:

.

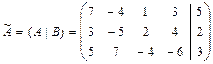2в)Выполняем прямой ход метода Гаусса.

.

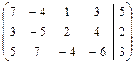
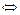
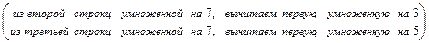
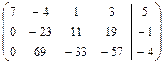
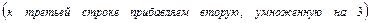
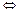
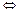
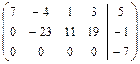При выполнении преобразования расширенной матрицы 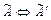, в преобразованной матрице 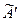появилась строка 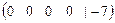, соответствующая уравнению 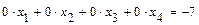, которому не удовлетворяет ни один набор значений неизвестных 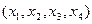, что говорит о несовместности исходной системы уравнений.

Ответ: Система несовместна.

5.1– 30.Даны векторы 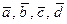: 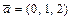; ; 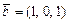; 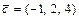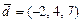. Требуется: а)вычислить скалярное произведение векторов 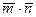, если 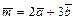, 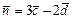; б)вычислить векторное произведение векторов 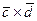; в)показать, что векторы 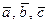образуют базис 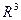и найти координаты вектора 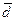в этом базисе.