Решение. 1а)Записываем расширенную матрицу системы:

1а)Записываем расширенную матрицу системы:

.

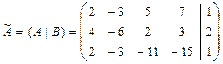2а)Выполняем прямой ход метода Гаусса.

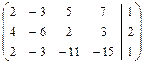
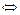
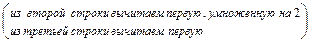
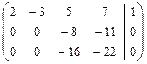
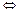
Замечание. В результате прямого хода матрица системы 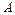должна быть преобразована с помощью элементарных преобразований строк к матрице 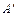треугольного или трапециевидного вида с элементами .

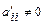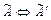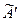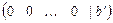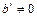Если, при выполнении преобразования расширенной матрицы , в преобразованной матрице появляется строка , где , то это говорит о несовместности исходной системы уравнений.

Для выполнения условия 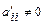может потребоваться перестановка местами столбцов матрицы системы. Если при выполнении преобразований прямого хода в матрице системы переставлялись местами столбцы коэффициентов при неизвестных, то в дальнейшем, при записи системы уравнений, соответствующей последней расширенной матрице прямого хода, это следует учесть.

.

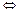
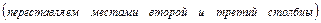
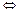
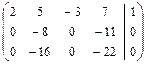
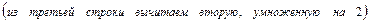
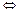
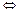
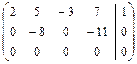
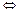
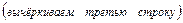
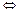
Матрица системы приведена к трапециевидному виду с ненулевыми диагональными элементами. Соответствующая такой матрице система уравнений имеет бесконечно много решений, которые находим, выполняя обратный ход, и записываем в виде общего решения. Для записи общего решения указываем её базисные и свободные неизвестные. Базисный минор матрицы системы, с учётом перестановки местами столбцов, образуют первый и второй столбцы коэффициентов при неизвестных 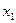и 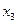: 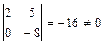. Поэтому выбираем в качестве базисных – неизвестные 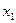и 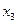, тогда свободными будут неизвестные 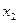и .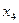

3б)Выполняем обратный ход метода Гаусса.

Записываем систему уравнений, соответствующую последней расширенной матрице прямого хода: 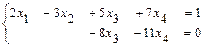. Свободным неизвестным придаём разные, произвольные постоянные значения: 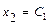, , 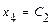и последовательно из уравнений системы, начиная с последнего, находим значения всех базисных неизвестных: .

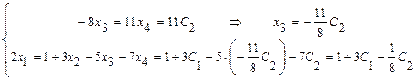Тогда общее решение системы запишется в виде:

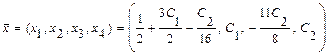
4б) Выполняем проверку:

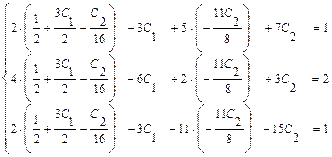
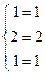
Ответ: .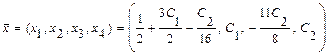

В) .