Раздел V. Комплексные числа. Алгебра многочленов.
Комплексное число, его изображение на плоскости. Комплексно-сопряжённое число. Модуль и аргумент комплексного числа. Различные формы записи комплексного числа (алгебраическая, тригонометрическая, показательная). Формула Эйлера.
Действия над комплексными числами (сложение, вычитание, умножение, деление) в алгебраической, тригонометрической и показательной формах.
Возведение комплексного числа в степень. Формула Муавра. Извлечение корня из комплексного числа.
Понятие многочлена, алгебраического уравнения. Основная теорема алгебры и теорема Безу. Разложение многочлена на множители. Нахождение корней квадратного уравнения.
Приложения.
Образец решения контрольных задач типового варианта.
1.1 – 30.Вычислить определитель: 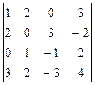
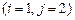
а)непосредственным разложением по 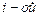 строке;
строке;
б)непосредственным разложением по 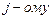 столбцу;
столбцу;
Решение. а)вычисляем определитель разложением по элементам первой строки: 
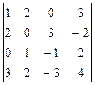 =
= 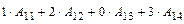 .
.
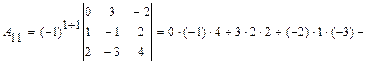
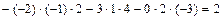
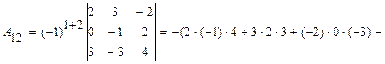
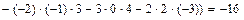
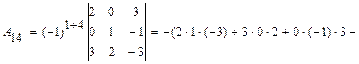
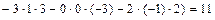
Тогда 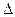 =
= 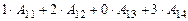 =
= 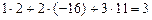
б)вычисляем определитель непосредственным разложением по элементам второго столбца: 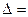
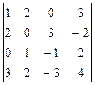 =
= 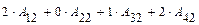 .
.
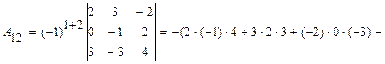
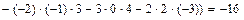
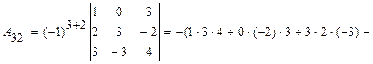
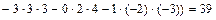
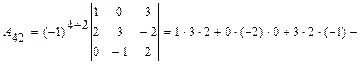
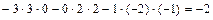
Тогда 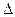 =
= 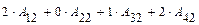 =
= 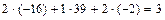 .
.
Дата добавления: 2014-12-04; просмотров: 981;
