Раздел IV. Введение в анализ.

Понятие множества. Подмножество. Универсальное множество. Способы задания множеств. Равенство и эквивалентность множеств.

Пересечение, объединение и разность множеств. Дополнение множества. Множества чисел.

Модуль действительного числа и его свойства.

Числовые промежутки. Окрестность конечной точки и бесконечности.

Понятие функции. Основные способы задания функции. Естественная область определения функции. Явная, неявная и параметрическая формы аналитического задания функции. График функции.

Основные элементы поведения функции (чётность, нечётность, периодичность, ограниченность, монотонность).

Основные элементарные функции (степенные: 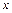, , 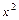, , 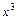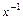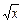; тригонометрические: 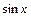, , 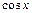, 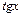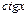; обратные тригонометрические: 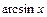, , 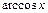, 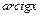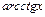; показательная 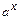, логарифмическая 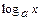), их свойства и графики.

Понятие обратной и сложной функций. Элементарные функции, их классификация. Преобразование графиков элементарных функций.

Понятие предела функции в конечной точке и на бесконечности, их геометрический смысл. Односторонние пределы. Условия существования предела функции в конечной точке.

Бесконечно малые и большие функции, их основные свойства и взаимосвязь. Примеры бесконечно малых и больших функций.

Функции, ограниченные при 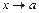. Взаимосвязь между функциями, имеющими предел и ограниченными при .

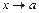Основные теоремы о пределах функций (о пределе постоянной, суммы, разности, произведения и частного функций; о пределе сложной и элементарной функций). Предельный переход в неравенствах.

Первый и второй замечательные пределы, их следствия и применение при вычислении пределов.

Эквивалентные бесконечно малые функции, их основные свойства и применение при вычислении пределов.

Определения непрерывности функции в точке. Понятие непрерывности справа и слева. Условия непрерывности функции в точке. Арифметические операции над непрерывными функциями.

Непрерывность сложной функции. Непрерывность элементарных функций. Условие существования непрерывной обратной функции.

Понятие непрерывности на отрезке. Свойства функций непрерывных на отрезке (об ограниченности функции, об обращении функции в нуль, о наибольшем и наименьшем значениях функции).

Точки разрыва функции, их классификация и нахождение.