Параметрів настройок регуляторів
Пояснимо графо-аналітичний метод розрахунку опримальних параметрів настройки регулятора на прикладі АСР з ПІ-регулятором.
1) Будуємо на міліметровому аркуші формату А3 в певному масштабі АФХ розімкненої системи ( 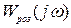 з пропорційним регулятором, для якого приймаємо
з пропорційним регулятором, для якого приймаємо 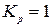 . В цьому випадку годограф
. В цьому випадку годограф 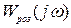 накладається на годограф об’єкта за каналом управління
накладається на годограф об’єкта за каналом управління  (див. рис. 3.2). На годографі відмічаємо частоти
(див. рис. 3.2). На годографі відмічаємо частоти  (приблизно 6…8 значень):
(приблизно 6…8 значень):
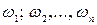 .
.
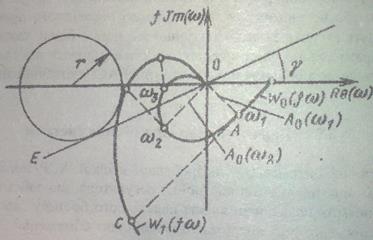
Рис. 3.2. Визначення границі заданого запасу стійкості АСР графо-аналітичним методом.
2) Для кожної з частот 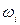 провести вектор ОАі.
провести вектор ОАі.
3) За частотною характеристикою 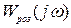 побудувати сімейство частотних характеристик розімкненої системи з ПІ-регулятором, для якої
побудувати сімейство частотних характеристик розімкненої системи з ПІ-регулятором, для якої  та є декілька значень часу інтегрування
та є декілька значень часу інтегрування 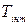 .
.
Щоб задатися 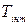 , визначаємо сталу часу
, визначаємо сталу часу 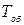 з кривої розгону об’єкта за каналом управління та задаємося інтервалом зміни
з кривої розгону об’єкта за каналом управління та задаємося інтервалом зміни 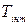 (
( 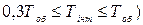 . На інтервалі обираємо 6…8 значень
. На інтервалі обираємо 6…8 значень 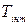 . Tоб=63 (с) 19<Tінт<63
. Tоб=63 (с) 19<Tінт<63
Tінт1=19; Tінт2=28; Tінт3=37; Tінт4=46; Tінт5=55; Tінт6=63;
4) До кожного вектора ОАі проводиться вектор під кутом 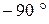 , на якому відкладаються відрізки довжиною:
, на якому відкладаються відрізки довжиною:
 .
.
Отримуємо ряд векторів. Точки Сі з’єднуємо плавними кривими. Кожна крива буде частотною характеристикою розімкненої системи з ПІ-регулятором 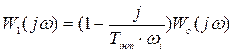 і буде відрізнятися від іншої тільки часом інтегрування
і буде відрізнятися від іншої тільки часом інтегрування 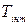 .
.
ОА1=21,3 (см); ОА2=16,8 (см); ОА3=14 (см);
ОА4=11,2 (см); ОА5=9,2 (см); ОА5=7,2 (см);
| 28,7 | 19,5 | 14,8 | 11,9 | 9,9 | 8,7 |
| 17,7 | 9,1 | 7,3 | 6,1 | 5,1 | |
| 12,3 | 8,3 | 6,3 | 5,1 | 4,2 | 3,5 |
| 8,4 | 5,7 | 4,3 | 3,5 | 2,9 | 2,4 |
| 4,1 | 3,1 | 2,5 | 2,1 | 1,7 | |
| 4,2 | 2,8 | 2,2 | 1,7 | 1,4 | 1,2 |
5) Провести пряму ОЕ під кутом 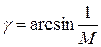 , де
, де 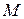 – величина, пов’язана з показником коливальності системи, який визначається як відношення модуля АФХ замкненої системи за резонансної частоти
– величина, пов’язана з показником коливальності системи, який визначається як відношення модуля АФХ замкненої системи за резонансної частоти 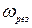
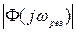 до модуля АФХ замкненої системи за частоти
до модуля АФХ замкненої системи за частоти 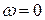
 –
– 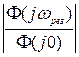 . За
. За 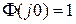 показник коливальності співпадає з величиною
показник коливальності співпадає з величиною 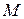 .
.
Залежність між ступенем затухання, резонансним піком модуля АФХ замкненої системи, кутом 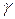 та величиною
та величиною 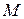 наведена у таблиці [4]:
наведена у таблиці [4]:
| Ступінь затухання | 0,70 | 0,75 | 0,80 | 0,85 | 0,90 | 0,95 |
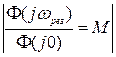
| 2,70 | 2,38 | 2,09 | 1,80 | 1,55 | 1,29 |
Кут 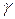 , град. , град.
| 21,7 | 24,8 | 28,6 | 33,8 | 40,2 | 50,8 |
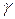 =28,6; М=2,09;
=28,6; М=2,09; 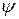 =0,8;
=0,8;
6) Шляхом підбору провести коло з центром на осі абсцис і радіусом  , яке торкається одночасно прямої ОЕта
, яке торкається одночасно прямої ОЕта 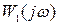 для заданого
для заданого 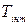 .
.
Виміряти радіус  лінійкою та отримані значення перевести з мм в
лінійкою та отримані значення перевести з мм в  .
.
 =
= 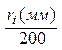 ;
;
7) Для заданого 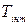 коефіцієнт передачі регулятора визначаємо за формулою:
коефіцієнт передачі регулятора визначаємо за формулою:
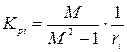 ;
;
K1=0,7 K2=1,18 K3=1,5 K4=1,7 K5=1,9 K6=2,1
Tінт1=19; Tінт2=28; Tінт3=37; Tінт4=46; Tінт5=55; Tінт6=63;
8) За отриманими результатами будуємо в площині параметрів настроювання регулятора 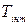 та
та 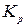 границю області заданого запасу стійкості, типовий вигляд якої наведено на рис. 3.3.
границю області заданого запасу стійкості, типовий вигляд якої наведено на рис. 3.3.
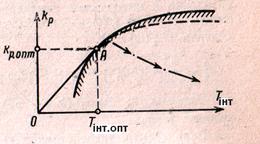
Рис. 3.3. Границя заданого запасу стійкості для системи з ПІ-регулятором
Максимум відношення 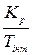 , який визначає оптимальну настройку регулятора за низькочастотних збурень, що відповідає точці дотику дотичної до границі заданого запасу стійкості, проведеної з початку координат (точка А на рис. 3.3).
, який визначає оптимальну настройку регулятора за низькочастотних збурень, що відповідає точці дотику дотичної до границі заданого запасу стійкості, проведеної з початку координат (точка А на рис. 3.3).
9) Встановлюємо отримані оптимальні значення настройок до змодельованої АСР і отримуємо перехідний процес, прямі показники якості якого мають підтвердити проведені розрахунки за умови дії збурень, величина яких задана у вихідних даних, та зміни завдання.
Xзад=10 
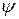 =0,8;
=0,8; 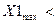 12
12  ;
; 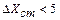
 ;
; 
Розрахунок оптимальних параметрів:
Ki1=0.0368
Ki2=0.0421
Ki3=0.0405
Ki4=0.0369
Ki5=0.0345
Ki6=0.0333
Максимум відношення 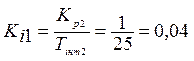 ;
;
Після отримання оптимальних настройок для системи (рис. 15) отримуємо перехідний процес (рис. 16), який має такі якісні показники:
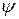 =0,8; А1=
=0,8; А1= 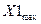 =4
=4  ;
; 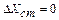
 ;
;
Ці показники досягли при таких значеннях настройки регулятора:
Кр=1,25; Кі=0,044;
Отриманий перехідний процес задовольняє вихідні характеристики щодо якості: 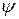 =0.8;
=0.8; 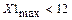
 ;
; 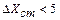
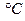 ;
;
На рис. 17,18 зображені перехідні процеси при +20% ПІ-складової, ти при -20% ПІ-складової.
Дата добавления: 2014-12-01; просмотров: 1387;
